生成模型以及扩散模型原理推导

美国科罗拉多州技术博览会中获得数字艺术类冠军的作品——《太空歌剧院》

美国科罗拉多州技术博览会中获得数字艺术类冠军的作品——《太空歌剧院》

最近爆火的AI绘图，相信大家并不陌生了。本文讨论的是最近在生成模型中逐渐受到重视的扩散模型DDPM（全称Denoising Diffusion Probabilistic Models)。由于扩散模型相较于普通的深度学习模型，数学难度大很多，因此该模型理解起来非常吃力。本文主要根据B站Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解以及博客What are Diffusion Models?中的讲解，同时加上一些数学基础知识和自己的理解，欢迎指正。

1 概率生成模型基本思想

散度最小化是生成模型的一般框架。我们可以将我们的训练集看作是对某个高维空间$\Omega$中的一个随机向量$X$进行多次采样得到的结果，这个随机向量服从一个未知的概率分布$P_r$。那么我们可以通过$X$的样本集（即训练集）来学习获得一个参数化模型$P_\theta$，此时学习获得的模型$P_\theta$应当与$P_r$是近似的，之后通过学习到的模型$P_\theta$再进行采样，则就能获得与训练集近似分布的生成结果，这便是生成网络的基本思想。
然而在实际操作中，由于待拟合的概率分布$P_r$往往非常复杂，神经网络通常很难直接拟合，且另一方面生成的结果很难量化评估其好坏，因此并不能简单地去构造一个生成网络来解决问题。

生成模型-GAN、生成模型-VAE和生成模型-Flow based model在生成高质量样本方面显示出巨大的成功，但每一种都有其自身的一些局限性。下面是对GAN、VAE和基于流的生成模型之间区别的一个快速总结。

生成对抗网络。GAN提供了一个聪明的解决方案，将数据生成这一无监督的学习问题建模为有监督的问题。鉴别器模型学习从生成器模型产生的虚假样本中区分出真实数据。两个模型同时训练，进行最大最小博弈。但是训练不稳定，多样性较少。
变量自动编码器。VAE通过最大化证据下限（ELBO），不明确地优化了数据的对数可能性。但是依赖于surrogate loss。
基于流的生成模型。基于流的生成模型是由一连串的可逆变换构建的。与其他两种不同，该模型明确地学习了数据分布，因此损失函数只是负对数似然。需要使用专门的架构来构建可逆变换。
扩散模型是受非平衡热力学的启发。它们定义一个扩散步骤的马尔可夫链，逐渐向数据添加随机噪声，然后学习逆扩散过程，从噪声中构建所需的数据样本。与VAE或流动模型不同，扩散模型是用固定的程序学习的，而且隐变量具有高维度（与原始数据相同）。

现有的生成模型可以根据如何表示概率分布分为以下两类：

基于似然的模型，通过（近似）最大似然直接学习分布的概率密度（或质量）函数。典型的基于似然的模型包括自回归模型，归一化流模型, 基于能量的模型 (EBM)和变分自动编码器 (VAE)。
隐式生成模型，其概率分布由其采样过程的模型隐式表示。最突出的例子是生成对抗网络（GAN），其中来自数据分布的新样本是通过用神经网络转换随机高斯向量来合成的。

2 条件概率公式

条件概率的一般形式：
$$
P(A,B,C)=P(C\mid A,B)P(A,B)=P(C\mid A,B)P(B\mid A)P(A) \
P(B,C\mid A)=P(B\mid A)P(C\mid A,B)
$$
隐马尔可夫模型(HMM,Hidden Markov Model)的两个基本假设：

齐次马尔可夫性假设：隐藏的马尔可夫链在时刻$t$的状态只和$t -1$的状态有关。
$$
P\left(i_t \mid i_{t-1}, o_{t-1}, \ldots, i_1, o_1\right)=P\left(i_t \mid i_{t-1}\right), \quad t=1,2, \ldots, T
$$
观测独立性假设：观测只和当前时刻的状态有关。
$$
P\left(o_t \mid i_T, o_T, i_{T-1}, o_{T-1}, \ldots, i_{t+1}, o_{t+1}, i_t, i_{t-1}, o_{t-1}, \ldots, i_1, o_1\right)=P\left(o_t \mid i_t\right)
$$

基于马尔科夫链的关系$A → B → C$,则有：

$$
P(A,B,C)=P(C\mid A,B)P(A,B)=P(C\mid B)P(B\mid A)P(A)$,$P(B,C\mid A)=P(B\mid A)P(C\mid B)
$$

3 高斯分布的KL散度

KL散度（Kullback Leibler Divergence）在概率模型中一般用于度量两个概率密度函数之间的“距离”，其定义为

$K L[p(X) | q(X)]=E_{x \sim p(X)}\left[\log \left(\frac{p(X)}{q(X)}\right)\right]= \begin{cases}\sum_{x \in X}\left[p(x) \log \left(\frac{p(x)}{q(x)}\right)\right], & x \sim p(X) \text { 为离散概率分布 } \ \int_{i \in X} p(x) \log \left(\frac{p(x)}{q(x)}\right) d x, & x \sim p(X) \text { 为连续概率分布 }\end{cases}$

由Jensen’s Inequality可以证明KL散度必然大于等于0。注意到KL散度的定义中$ KL[p(X)||q(X)]$关于 $p(X)$、 $q(X)$ 并不对称，即 $KL[p(X) ||q(X)]$ , $KL[q(X)||p(X)]$ ，因此KL散度不满足对称性，显然不是数学意义上的“度量”。在优化问题中，常用 $p(X)$ 表示真实分布，$q (X)$ 表示一个用于拟合 $p (X)$ 的近似分布，在这种情形下，通常称 $KL[p (X) ||q (X)]$ 为前向KL散度（forward Kullback Leibler Divergence），而称$ KL[q (X) ||p (X)] $为反向KL散度（reverse Kullback Leibler Divergence）。

4 重参数化

重参数化又称参数重整化，若希望从某个高斯分布$N(\mu,\sigma^2)$分布中随机采样一个样本，这个过程是无法反传梯度的。可以先从标准分布$N(0,1)$采样出$z$，再得到$ \sigma * z + \mu$。这样做的好处是将随机性转移到了 $z$ 这个常量上，而 $\sigma$ 和 $\mu$ 则当做仿射变换网络的一部分，整个“采样”过程依旧梯度可导。

import torch

def reparametrize(mean,lg_var): # 采样器方法：对方差(lg_var)进行还原，并从高斯分布中采样，将采样数值映射到编码器输出的数据分布中。
        std = lg_var.exp().sqrt()
        # torch.FloatTensor(std.size())的作用是，生成一个与std形状一样的张量。然后，调用该张量的normal_()方法，系统会对该张量中的每个元素在标准高斯空间（均值为0、方差为1）中进行采样。
        eps = torch.FloatTensor(std.size()).normal_() # 随机张量方法normal_()，完成高斯空间的采样过程。
        return eps.mul(std).add_(mean)

5 VAE

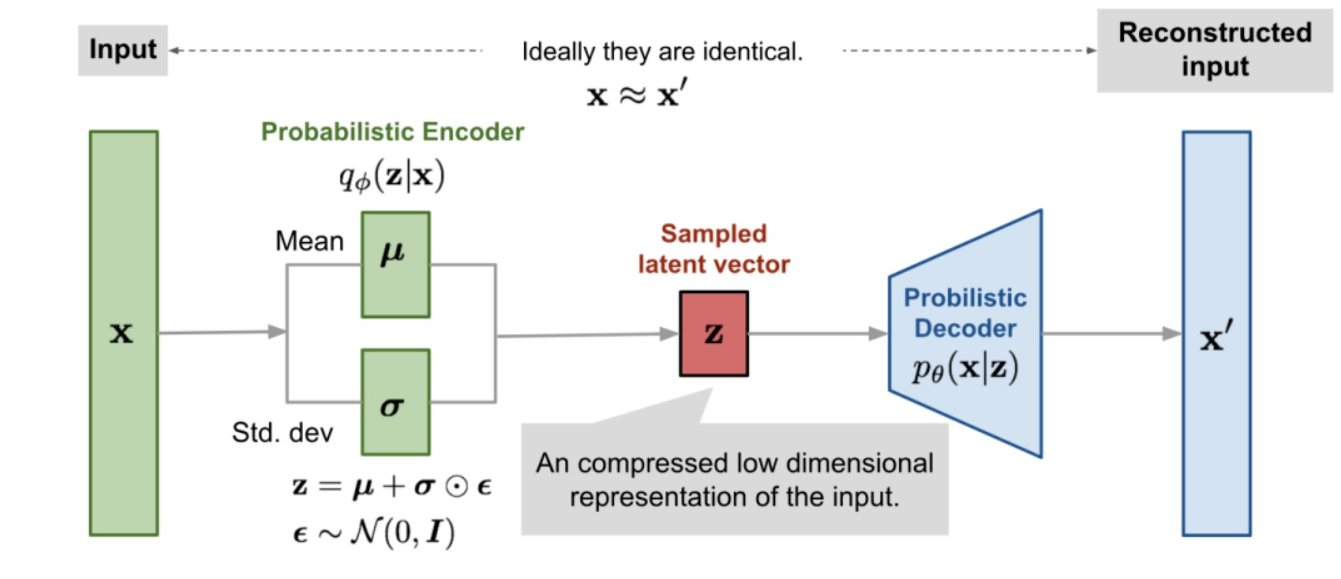
VAE整体可以看作encoder-decoder架构。对于一个输入的向量 $x$，它通常包含了许多冗余信息，我们要还原生成这个向量 $x$ 实际上更需要的是描述其本质信息的隐变量 $z$，因此使用了encoder-decoder架构来设计网络，用encoder来进行 $x → z$ 的编码过程，而decoder则用于 $z → x$ 的生成过程。

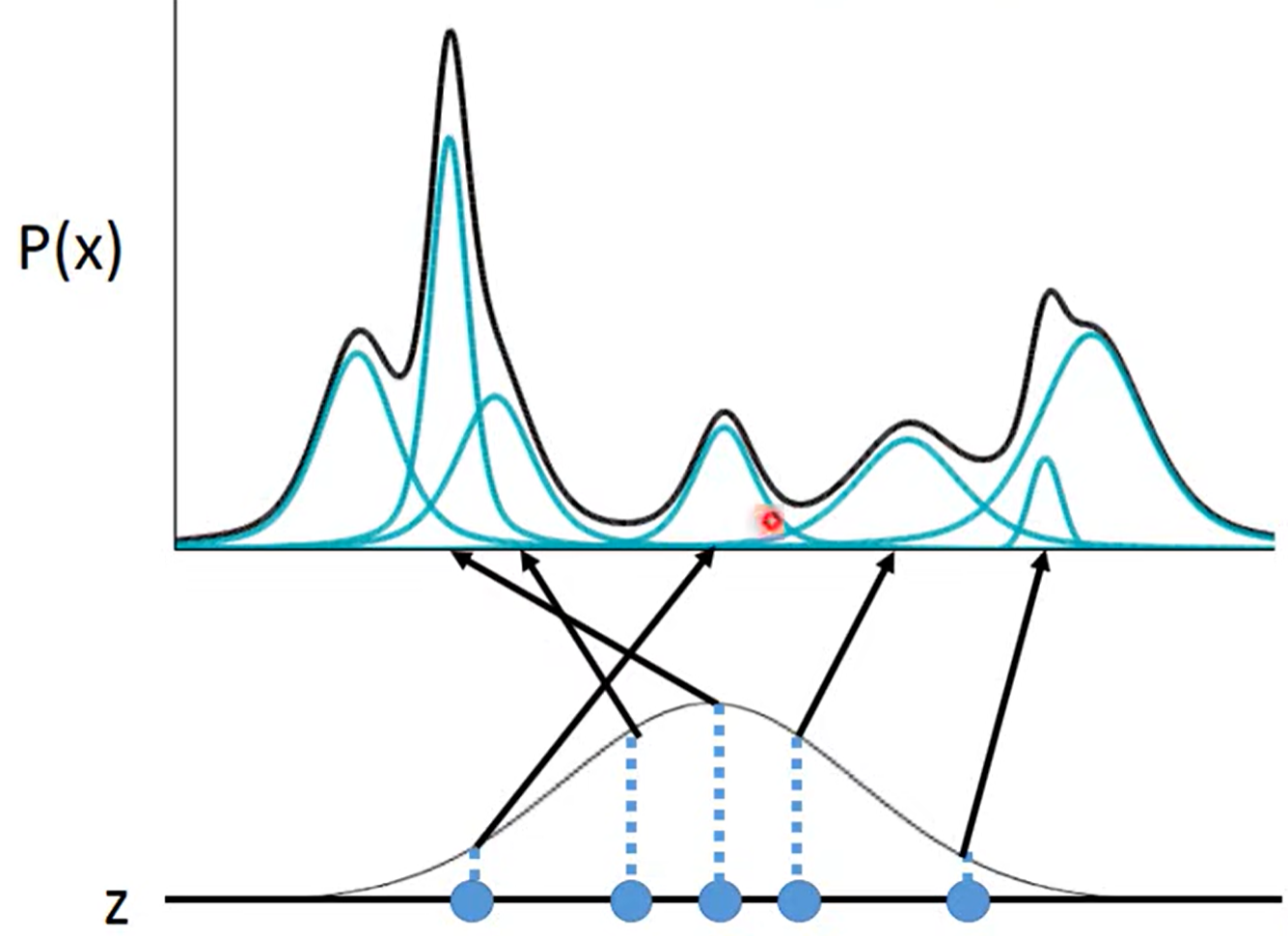
首先考虑网络的decoder，即生成部分。如图所示，由于目标概率密度函数 $p_r (X)$ 通常并不是一个上凸函数，它通常会具有多个极值，所以我们可以考虑使用多个高斯分布相叠加去拟合概率密度函数 $p_r (X)$，这个思想就是高斯混合模型的思想。我们将隐变量 $Z$ 看作一个随机变量，我们对隐变量 $Z$ 的每个可能的取值，都将其放入一个映射来得到一个均值 $\mu (z)$ 和一个标准差 $\sigma(z)$，此时我们便可以从这个隐变量的每个取值分别获得一个高斯分布 $N(\mu(z),\sigma^2(z))$ 。因此，如果我们假设 $Z$ 服从某个概率分布，那么对于概率密度函数 $p (X)$，我们有$p(x)=\int_z p(z) p(x\mid z) dz$，其中 $p (X\mid Z)$ 服从高斯分布 $X|Z ∼ N(\mu(Z),\sigma^2(Z))$ ，这个 $p (X \mid Z)$ 便是 $z → x$的结构，即VAE中的decoder结构。如果我们将 $Z$ 的概率分布确定下来为某个已知分布，那么概率密度函数 $p (X)$ 就仅与映射 $\mu$ 和 $\sigma$ 相关了。在VAE中我们假设 $Z$ 的概率分布为 $Z ∼ N (0, 1)$。

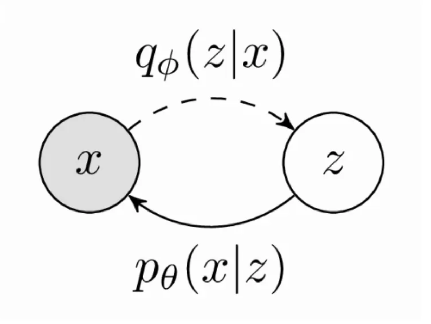
现在再来尝试推导出网络的encoder结构。由于我们的目标是在训练集上最大化$\sum_x \log p(x)$，我们假设 $Z \mid X$上有一个任意的概率密度函数 $q(Z \mid X)$，对 $ \log p(X)$ 做变换我们有：

$$
\begin{aligned} \log p(x) & =\log p(x) \cdot \int_z q(z \mid x) d z \ & =\int_z q(z \mid x) \log p(x) d z \ & =\int_z q(z \mid x) \log \left(\frac{p(z, x)}{p(z \mid x)}\right) d z \ & =\int_z q(z \mid x) \log \left(\frac{p(z, x)}{q(z \mid x)} \cdot \frac{q(z \mid x)}{p(z \mid x)}\right) d z \ & =\int_z q(z \mid x) \log \left(\frac{p(z, x)}{q(z \mid x)}\right) d z+\int_z q(z \mid x) \log \left(\frac{q(z \mid x)}{p(z \mid x)}\right) d z \ & =\int_z q(z \mid x) \log \left(\frac{p(x \mid z) p(z)}{q(z \mid x)}\right) d z+K L[q(z \mid x) | p(z \mid x)]\end{aligned}
$$
我们记$L_b=\int_z q(z \mid x) \log \left(\frac{p(x \mid z) p(z)}{q(z \mid x)}\right) dz$，则我们便得到了如下式子（即置信下界）：
$$
\log p(x)=L_b+K L[q(z \mid x) | p(z \mid x)] \geq L_b
$$
此时很直观地，我们似乎只要调整 $p(x\mid z)$ 和 $q(z\mid x)$ 来将 $L_b$ 最大化即可将 $ \log p (x)$ 最大化了，但由于 $p(z\mid x)$ 与 $p (x\mid z)$ 相关联，在调整 $p (x\mid z)$ 的时候可能会导致 $KL [q (z\mid x) ||p (z\mid x)]$ 下降从而导致 $\log p (x)$ 反而下降，而由于 $q (z\mid x)$ 为任意概率密度函数，它变化时并不会导致 $p$ 变化，因此我们考虑先把 $p (x\mid z)$ 固定（此时 $\log p (x) = log(\int_z p(z)p(x|z)dz)$ 也会固定），仅调整 $q (z\mid x)$。显然，当 $q (z\mid x)$ 逼近$p(z\mid x)$时，$KL[q (z\mid x) ||p (z\mid x)]$ 会趋近于0，此时$\log p (x)$ 会趋近于 $L_b$，因此，在将 $q (z\mid x)$ 逼近 $p (z\mid x)$ 的情况下再通过调整 $p (z\mid x)$ 来增大 $L_b$ 时， $\log p (x)$ 也会随之增大。而对于 $L_b$，我们有
$$
\begin{aligned}
L_b & =\int_z q(z \mid x) \log \left(\frac{p(x \mid z) p(z)}{q(z \mid x)}\right) d z \
& =\int_z q(z \mid x) \log p(x \mid z) d z+\int_z q(z \mid x) \log \left(\frac{p(z)}{q(z \mid x)}\right) d z \
& =E_{Z \sim q(z \mid x)}[\log p(x \mid z)]-K L[q(z \mid x) | p(z)]
\end{aligned}
$$
注：随机变量的数学期望，设X是随机变量，$Y$是$X$的函数，$Y=g(X)$($g$为连续函数).如果$X$是连续型随机变量,其概率密度为$f(x)$。若积分$\int_{-\infty}^{+ \infty} xf(x)dx$绝对收敛，则称X的数学期望存在，且$E(x)= \int_{-\infty}^{+ \infty} x f(x)d x$。

此时我们便得到了我们最终所需的表达式：
$$
\log p(x)=E_{Z \sim q(z \mid x)}[\log p(x \mid z)]-K L[q(z \mid x) | p(z)]+K L[q(z \mid x) | p(z \mid x)]
$$

我们来逐个解析表达式中的三项内容：

$K L[q(z \mid x) | p(z \mid x)]$

在上文中我们已经提到，我们要最大化$\log p(x)$就会希望极小化$K L[q(z \mid x) | p(z \mid x)]$，这便意味着我们希望使用$q(z\mid x)$去逼近$p(z\mid x)$，即使用$q(z\mid x)$来作为网络的encoder部分。
$K L[q(z \mid x) | p(z)]$

要最大化$\log p(x)$，则$K L[q(z \mid x) | p(z)]$就需要尽可能的小，而这项KL散度的直观含义也很明显，即我们希望$x → z$的过程中产生的$Z$的分布$q(z\mid x)$尽可能与我们假设的$Z$的分布$p(z)$相似，当 $q (z\mid x)$ 逼近$p(z)$时，$KL[q (z\mid x) ||p (z)]$ 会趋近于0，因此encoder部分还需要满足其概率分布为预先假设的 $Z$ 的分布。
$E_{Z \sim q(z \mid x)}[\log p(x \mid z)]$

最大化$\log p(x)$显然就会需要最大化期望$E_{Z \sim q(z \mid x)}[\log p(x \mid z)]$，而最大化这项期望的直观含义也很明显，我们希望在给定encoder输出$q(z\mid x)$的情况下，decoder的输出$\log p(x\mid z)$的均值尽可能的大，即 $p(x\mid z)$的均值尽可能的大。

现在对照网络结构图，显然 $q (z\mid x)$ 对应的即为网络encoder部分，它需要去近似 $Z$ 的分布，而根据我们对 $p (z)$ 的假设， $q (z|x)$ 将会趋近于一个标准正态分布，此时对 $q (z|x)$ 进行采样便可以得到 $z$，并传入decoder部分。网络的decoder部分则为最开始所说的 $p (x|z)$，即 $X|Z ∼N(\mu (Z) , \sigma^2 (Z))$ ，用于使用高斯分布的输出去近似数据分布。

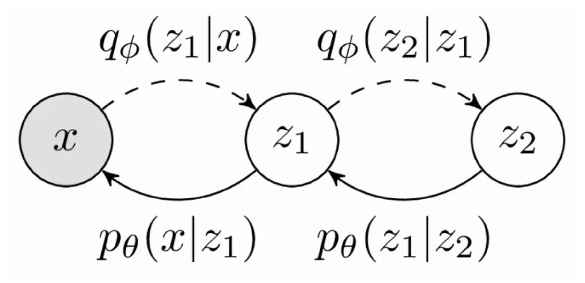
对于多层VAE及其置信下界，同理我们可以写成：
$$
\begin{aligned}
\log p(x) & =\log p(x) \cdot \iint q(z_1,z_2 \mid x) d z_1 d z_2 \
& =\iint q(z_1,z_2 \mid x) \log p(x) d z_1 d z_2 \
& =\iint q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2, x)}{p(z_1,z_2 \mid x)}\right) d z_1 d z_2 \
& =\iint q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2, x)}{q(z_1,z_2 \mid x)} \cdot \frac{q(z_1,z_2 \mid x)}{p(z_1,z_2 \mid x)}\right) d z_1 d z_2 \
& =\iint q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2, x)}{q(z_1,z_2 \mid x)}\right) d z_1 d z_2 +\iint q(z_1,z_2 \mid x) \log \left(\frac{q(z_1,z_2 \mid x)}{p(z_1,z_2 \mid x)}\right) d z_1 d z_2 \
&(=\iint q(z_1 \mid x) q(z_2 \mid z_1,x) \log \left(\frac{p(x \mid z_1,z_2) p(z_1 \mid z_2) p(z_2)}{q(z_1 \mid x) q(z_2 \mid z_1,x)}\right) d z_1 d z_2 + \iint q(z_1 \mid x) q(z_2 \mid z_1,x) \log \left(\frac{q(z_1 \mid x) q(z_2 \mid z_1,x))}{p(z_1,z_2 \mid x)}\right) d z_1 d z_2) \
&(=\iint q(z_1 \mid x) q(z_2 \mid z_1) \log \left(\frac{p(x \mid z_1) p(z_1 \mid z_2) p(z_2)}{q(z_1 \mid x) q(z_2 \mid z_1)}\right) d z_1 d z_2+\iint q(z_1 \mid x) q(z_2 \mid z_1) \log \left(\frac{q(z_1 \mid x) q(z_2 \mid z_1))}{p(z_1,z_2 \mid x)}\right) d z_1 d z_2)\end{aligned}
$$

记 $L_b=\iint q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2, x)}{q(z_1,z_2 \mid x)}\right) d z_1 d z_2$，则有

$$
\begin{aligned}\log p(x)=L_b+K L[q(z_1,z_2 \mid x) | p(z_1,z_2 \mid x)] \geq L_b\end{aligned}
$$

$$
\begin{aligned}
L_b & =\iint q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2, x)}{q(z_1,z_2 \mid x)}\right) d z_1 d z_2 \
& (=\iint_z q(z_1,z_2 \mid x) \log p(x \mid z_1,z_2) d z_1 d z_2+\iint_z q(z_1,z_2 \mid x) \log \left(\frac{p(z_1,z_2)}{q(z_1,z_2 \mid x)}\right) d z_1 d z_2) \
& =\iint_z q(z_1,z_2 \mid x) \log \left(\frac{p(x\mid z_1,z_2)p(z_1\mid z_2)p(z_2)}{q(z_1\mid x)q(z_2\mid z_1,x)}\right) \
& =\iint_z q(z_1,z_2 \mid x) \log \left(\frac{p(x\mid z_1)p(z_1\mid z_2)p(z_2)}{q(z_1\mid x)q(z_2\mid z_1)}\right) \
& =\iint_z q(z_1,z_2 \mid x) \log [p(x\mid z_1)-\log q(z_1\mid x)+\log p(z_1\mid z_2)-\log q(z_2\mid z_1)+\log p(z_2)] \
& =E_{Z\sim q(z_1,z_2\mid x)}[\log p(x\mid z_1)-\log q(z_1\mid x)+\log p(z_1\mid z_2)-\log q(z_2\mid z_1)+\log p(z_2)]
\end{aligned}
$$

6 Diffusion Models

去噪扩散模型的想法已经存在了很长时间。它起源于扩散图概念，这是机器学习文献中使用的降维技术之一。它还借鉴了概率方法的概念，例如已在许多应用中使用的马尔可夫链。一些基于扩散的生成模型被提出，其下有类似的想法，包括扩散概率模型（DPM,Sohl-Dickstein et al., 2015），噪声条件得分网络（NCSN,Yang & Ermon, 2019），以及去噪扩散概率模型（DDPM,Ho et al. 2020）。

去噪扩散建模是一个两步过程：正向扩散过程和反向过程或重建。在前向扩散过程中，依次引入高斯噪声，直到数据全部变成噪声。反向/重建过程通过使用神经网络模型学习条件概率密度来消除噪声。

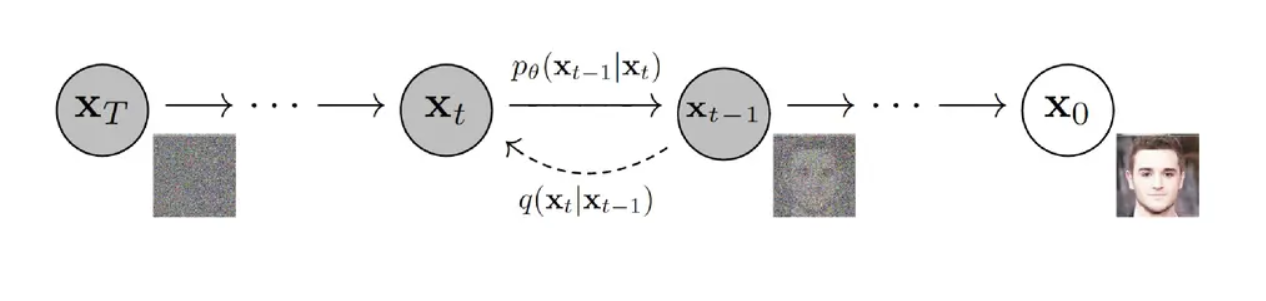
概率扩散模型的原理与VAE在某些地方有些相似。扩散模型如图所示，其中$X_0$是目标分布，$X_t$是噪声分布，扩散过程就是从$X_0$到$X_t$的过程，也就是熵增的过程从有序变无序，其实现原理是在源输入$X_0$上一步步的不断增加噪声，直到最后成为一个图像上各项独立分布，转变为随机噪声$X_T$；而生成过程则是一个相反的过程，其目的就是从随机噪声$X_T$分布中推理出目标分布，即还原源输入分布$X_0$，然后从目标分布中采样样本就能生成新的图像，也称为逆扩散过程。其中 $q(x_t\mid x_{t-1})$是扩散过程中的条件概率分布，$p(x_{t-1}\mid x_t)$是逆扩散过程的条件概率分布，在推理过程中只需要用到逆扩散过程的。

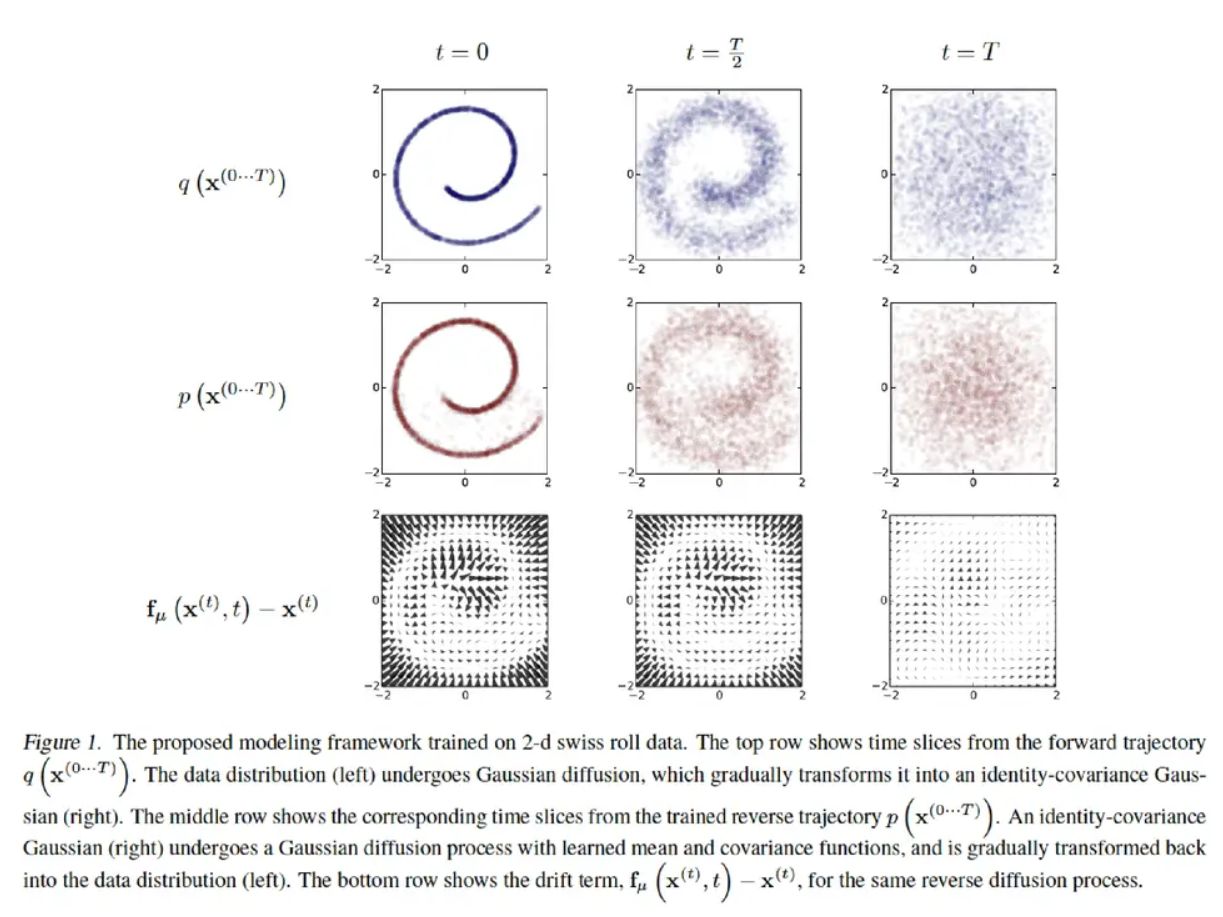
如图来表示扩散模型的过程，扩散过程就如第一行所示。对$t=0$规则的图像不断加噪，到$t= \frac {T}{2} $时我们可以看到图片已经模糊了，当$t=T$时我们发现图像已经变成了各项等与高斯分布。同理第二行展示的是逆扩散过程；第三行展示的就是在相同时刻扩散过程与逆扩散过程之间的差，即漂移量。

正向过程

我们先来讨论扩散过程，即正向过程。扩散过程实质上就是多次迭代向数据分布 $X_0 ∼ q(x)$ 中添加高斯噪声的一个马尔可夫链过程，因此，与 VAE 中的编码器不同，它不需要训练。从初始数据点开始，我们为$T$连续步骤添加高斯噪声，并获得一组噪声样本。时间$t$ 的概率密度预测仅取决于时间$t-1$的直接前驱，该噪声的标准差是以固定值$\beta_t$而确定的，均值是以固定值$\beta_t$和当前$t$时刻的数据$x_t$决定的。这个过程是固定的，且服从分布，因此，条件概率密度以及整个过程的完整分布可以计算如下：
$$
q\left(X_t \mid X_{t-1}\right)=N\left(X_t ; \sqrt{1-\beta_t} X_{t-1}, \beta_t I\right) \quad q\left(X_{1: T} \mid X_0\right)=\prod_{t=1}^T q\left(X_t \mid X_{t-1}\right)
$$
其中${\beta_t \in (0,1)}{_{t=1}^T}$ ，它是一个超参数，其值可以在整个过程中取为常数，也可以在连续的步骤中逐渐改变，且$\beta_t$的值是越来越大的。对于微分参数值分配，可以存在可用于对行为建模的函数范围（例如，sigmoid、tanh、linear等），$I$ 为单位矩阵。由于这个过程是确定的由于这个过程是确定的，因此任意时刻的分布 $q\left(X_t\right)$ 完全可以由 $X_0$ 及 $\beta_1,\beta_2,\cdots,\beta_t$ 确定，且随着$t$的不断增大，最终数据分布$x_T$变成了一个各项独立的高斯分布。

上述推导足以预测连续状态，但是，如果我们想在任何给定时间间隔$t$采样而不经过所有中间步骤，因此允许有效实现，那么我们可以重新制定进行推导，对 $X_t|X_{t-1}$，显然我们有
$$
\frac{X_t|X_{t-1}-\sqrt{1-\beta_t}X_{t-1}}{\sqrt{\beta_tI}}\sim N\left(0,I\right)
$$
设一系列 $\left{Z\sim N\left(0,I\right)\right}$ 以及设 $\alpha_t=1-\beta_t,\ \bar{\alpha}t=\prod\limits{i=1}^t\alpha_i$，基于前置参数重整化的知识此时我们可以从上式得到
$$
X_t|X_{t-1}=\sqrt{\alpha_t}X_{t-1}+\sqrt{1-\alpha_t}Z_{t-1}
$$
将上式中的 $X_{t-1}$ 替换为条件分布 $X_{t-1}|X_{t-2}$，则
$$
\begin{aligned}
X_t|X_{t-1}|X_{t-2}&=\sqrt{\alpha_t}\left(X_{t-1}|X_{t-2}\right)+\sqrt{1-\alpha_t}Z_{t-1}\
X_t|X_{t-1},X_{t-2}&=\sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}}X_{t-2}+\sqrt{1-\alpha_{t-1}}Z_{t-2}\right)+\sqrt{1-\alpha_t}Z_{t-1}\
X_t|X_{t-1},X_{t-2}&=\sqrt{\alpha_t\alpha_{t-1}}X_{t-2}+\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z_{t-2}+\sqrt{1-\alpha_t}Z_{t-1}\
X_t|X_{t-1},X_{t-2}&=\sqrt{\alpha_t\alpha_{t-1}}X_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}Z_{t-1,t-2}\
\end{aligned}
$$
注意：两个正态分布$X \sim N(\mu_1, \sigma_1)$和$Y \sim N(\mu_2,\sigma_2)$的叠加后的分布$aX +bY$的均值为$a\mu_1+ b\mu_2$，方差为$a^2\sigma_1^2+b^2\sigma_2^2$。所以$\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z_{t-2}+\sqrt{1-\alpha_t}Z_{t-1}$只是两个方差不一样，两方差求和开根号可以写成$\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z_{t-2}$，这样就可以重参数化成只含一个随机变量 $Z$ 构成的$\sqrt{1-\alpha_t\alpha_{t-1}}Z$的形式。

以此类推，最终我们可以得到
$$
X_t|X_{t-1},\cdots,X_0=\sqrt{\bar{\alpha}t}X_0+\sqrt{1-\bar{\alpha}t}Z{t-1,t-2,\cdots,0}
$$
即我们有
$$
q\left(X_t|X{0:\left(t-1\right)}\right)=N\left(X_t;\sqrt{\bar{\alpha}_t}X_0,\left(1-\bar{\alpha}_t\right)I\right)
$$
由于 $N\left(X_t;\sqrt{\bar{\alpha}t}X_0,\left(1-\bar{\alpha}t\right)I\right)$ 仅与 $X_0$ 有关，因此我们有
$$
q\left(X_t|X{0}\right)=N\left(X_t;\sqrt{\bar{\alpha}t}X_0,\left(1-\bar{\alpha}t\right)I\right)
$$
且有
$$
q\left(X_t|X{t-1}\right)=q\left(X_t|X{0:\left(t-1\right)}\right)=q\left(X_t|X{0}\right)
$$
显然，当 $\bar{\alpha}_t\to0$ 时，此时必然也有$(1-\bar{\alpha}t) \to 1 $， $q\left(X_t|X_0\right)$ 趋近于服从标准正态分布。通常情况下，当样本变得更加随机时，可以尝试更大的更新步骤，在DDPM原文中，作者将 $\left{\beta_t\right}{t=1}^{T}$ 设置为了线性增加的序列，即 $\beta_1<\beta_2<\cdots<\beta_T$,$\bar{\alpha}_1\gt\bar{\alpha}_2\gt\cdots \gt \bar{\alpha}_T$。

到这里我们就理解完了扩散模型的前向过程，这里我们可以将扩散模型的前向过程与VAE做一下对比，首先在VAE中从$X$到$Z$的过程并不是一个无参的过程，我们是通过一个后验网络预测出来的，其次$X$也并不是与$Z$无关。在扩散模型中$X_t$已经是一个各项独立的高斯正态分布。第二点区别是在VAE中$X$和$Z$的维度不一定是一样的，但是在扩散模型中，$X_0,X_1,\cdots,X_t$他们的维度始终是一致的。diffusion model和其他模型最大的区别是它的latent code(z)和原图是同尺寸大小的，当然最近也有基于压缩的latent diffusion model。

重构过程

接下来我们讨论逆扩散过程，也称反向过程或重构过程。逆向过程需要在给定系统当前状态的情况下，在较早的时间步估计概率密度，通俗理解就是要从高斯分布中恢复原始数据，这意味着在$t=T$时估计$q(X_{t-1} \mid X_t)$ ，从而从各向同性高斯噪声生成数据样本，在[文献](Feller, William. “On the theory of stochastic processes, with particular reference to applications.” Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1949.)中证明了如果 $q(X_t|X_{t−1})$ 满足高斯分布且 $\beta_t$ 足够小，$q(X_{t-1} \mid X_t)$仍然是一个高斯分布。

然而与前向过程不同，从当前状态估计先前状态需要所有先前梯度的知识，如果没有可以预测此类估计的学习模型，我们无法简单推断$q(X_{t-1} \mid X_t)$，因此我们使用深度学习模型（参数为 $\theta$ ，目前主流是U-Net+attention的结构），该模型去预测这样的一个逆向的分布 $p_\theta$（类似VAE），并且根据学习的权重$\theta$和时间$t$的当前状态来估计$p_\theta(X_{t-1}\mid X_t)$:
$$
p_{\theta}(X_{0:T})=p(X_T)\prod\limits_{t=1}^{T}p_{\theta}\left(X_{t-1}|X_t\right)
$$

$$
p_\theta\left(X_{t-1} \mid X_t\right)=\mathcal{N}\left(X_{t-1} ; \mu_\theta\left(X_t, t\right), \Sigma_\theta\left(X_t, t\right)\right)
$$

虽然我们无法得到逆转后的分布$q(X_{t-1} \mid X_t)$，但是如果知道$X_t$和$X_0$，是可以通过贝叶斯公式得到$X_{t-1}$为：
$$
q\left(X_{t-1}\mid X_t,X_{0}\right)=N(X_{t-1};\tilde \mu(X_t,X_0),\tilde \beta_t I)
$$
推导过程如下：
$$
\begin{aligned}
q\left(X_{t-1}|X_t,X_0\right)&=\frac{q\left(X_t,X_{t-1},X_0\right)}{q\left(X_t,X_0\right)}\
&=\frac{q\left(X_t|X_{t-1},X_0\right)q\left(X_{t-1},X_0\right)}{q\left(X_t,X_0\right)}\
&=\frac{q\left(X_t|X_{t-1}\right)q\left(X_{t-1},X_0\right)}{q\left(X_t,X_0\right)} (马尔科夫假设)\
&=q\left(X_t|X_{t-1}\right)\frac{q\left(X_{t-1}|X_0\right)}{q\left(X_t|X_0\right)}(巧妙地将逆向过程全部变回了前向)\
&=\frac{1}{\sqrt{2\pi}\cdot\frac{\sigma_{q\left(X_t|X_{t-1}\right)}\sigma_{q\left(X_{t-1}|X_0\right)}}{\sigma_{q\left(X_t|X_0\right)}}}\cdot e^{-\frac{1}{2}\left[\frac{\left(X_t-\sqrt{\alpha_t}X_{t-1}\right)^2}{\beta_t}+\frac{\left(X_{t-1}-\sqrt{\bar{\alpha}{t-1}}X_0\right)^2}{1-\bar{\alpha}{t-1}}-\frac{\left(X_t-\sqrt{\bar{\alpha}t}X_0\right)^2}{1-\bar{\alpha}t}\right]}\
&=\frac{1}{\sqrt{2\pi}\cdot\frac{\sigma{q\left(X_t|X{t-1}\right)}\sigma_{q\left(X_{t-1}|X_0\right)}}{\sigma_{q\left(X_t|X_0\right)}}}\cdot e^{-\frac{1}{2}\left[\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}{t-1}}\right)X{t-1}^2-\left(\frac{2\sqrt{\alpha_t}}{\beta_t}X_t+\frac{2\sqrt{\bar{\alpha}{t-1}}}{1-\bar{\alpha}{t-1}}X_0\right)X_{t-1}+C\left(X_t,X_0\right)\right]}\
&=\frac{1}{\sqrt{2\pi}\cdot\frac{\sigma_{q\left(X_t|X_{t-1}\right)}\sigma_{q\left(X_{t-1}|X_0\right)}}{\sigma_{q\left(X_t|X_0\right)}}}\cdot e^{-\frac{1}{2}\left[\frac{\left(X_{t-1}-\frac{\frac{\sqrt{\alpha_t}}{\beta_t}X_t+\frac{\sqrt{\bar{\alpha}{t-1}}}{1-\bar{\alpha}{t-1}}X_0}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}{t-1}}}\right)^2}{\frac{1}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}{t-1}}}}\right]+C^{\prime}\left(X_t,X_0\right)}\
&=\frac{1}{\sqrt{2\pi}\cdot\frac{\sigma_{q\left(X_t|X_{t-1}\right)}\sigma_{q\left(X_{t-1}|X_0\right)}}{\sigma_{q\left(X_t|X_0\right)}}}e^{C^{\prime}\left(X_t,X_0\right)}\cdot e^{-\frac{1}{2}\left[\frac{\left(X_{t-1}-\left(\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t}X_t+\frac{\sqrt{\bar{\alpha}t-1}\cdot\beta_t}{1-\bar{\alpha}t}X_0\right)\right)^2}{\frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}t}\beta_t}\right]}\
&=\frac{1}{\sqrt{2\pi}\cdot\sigma^{\prime}}\cdot e^{-\frac{1}{2}\left[\frac{\left(X{t-1}-\left(\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}{t-1}\right)}{1-\bar{\alpha}_t}X_t+\frac{\sqrt{\bar{\alpha}_t-1}\cdot\beta_t}{1-\bar{\alpha}t}X_0\right)\right)^2}{\frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}_t}\beta_t}\right]}\
\end{aligned}
$$
注意：高斯分布的概率密度函数是$f(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$, $ax^2+bx=a(x+{\frac {b}{2a}})^2+C$（韦达定理）

其中， $C\left(X_t,X_0\right)$ 和 $C^{\prime}\left(X_t,X_0\right)$ 均为某个仅与 $X_0$ 和 $X_t$ 有关的函数, $\sigma^{\prime}=\frac{\sigma_{q\left(X_t|X_{t-1}\right)}\cdot\sigma_{q\left(X_{t-1}|X_0\right)}}{\sigma_{q\left(X_t|X_0\right)}\cdot e^{C^{\prime}\left(X_t,X_0\right)}}$。显然，对均值为 $\tilde{\mu}t\left(X_t,X_0\right)=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}{t-1}\right)}{1-\bar{\alpha}_t}X_t+\frac{\sqrt{\bar{\alpha}_t-1}\cdot\beta_t}{1-\bar{\alpha}t}X_0$，并且由前面的式子以及参数重整化的知识我们可以进一步得到：
$$
q\left(X_t|X{0}\right)=N\left(X_t;\sqrt{\bar{\alpha}_t}X_0,\left(1-\bar{\alpha}_t\right)I\right) \to X_0=\frac{1}{\sqrt{\bar {\alpha}_t}}-\sqrt{1-\bar{\alpha}_t}\bar Z_t
$$
将$X_0$的表达式带入到均值的式子里，可以重新给出该分布的均值表达式，也就是说，在给定$X_0$的条件下，后验条件高斯分布的均值计算只与$X_t$和$Z_t$有关，$Z_t$是$t$时刻的随机正态分布变量，源自参数重整化。进一步我们可以将均值 $\tilde{\mu}_t\left(X_t,X_0\right)$ 记为：
$$
\tilde{\mu}t\left(X_t,X_0\right)=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}{t-1}\right)}{1-\bar{\alpha}_t}X_t+\frac{\sqrt{\bar{\alpha}_t-1}\cdot\beta_t}{1-\bar{\alpha}_t}(\frac{1}{\sqrt{\bar {\alpha}_t}}-\sqrt{1-\bar{\alpha}_t}Z_t)=\frac {1}{\sqrt{\alpha_t}}(X_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}\bar Z_t)
$$
其中高斯分布$\bar Z_t$为深度模型所预测的噪声（用于去噪），可看做为$Z_\theta\left(X_t, t\right)$ ，即得到：
$$
\mu_\theta\left(X_t, t\right)=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{a}_t}} Z_\theta\left(X_t, t\right)\right)
$$
由均值 $\tilde{\mu}_t\left(X_t,X_0\right)$ ，方差为 $\tilde{\beta}tI=\frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}t}\beta_t\cdot I$ 的正态分布 $N\left(X{t-1};\tilde{\mu}t\left(X_t,X_0\right),\tilde{\beta}tI\right)$，我们有
$$
\frac{q\left(X{t-1}|X_t,X_0\right)}{f{N\left(\tilde{\mu}_t\left(X_t,X_0\right),\tilde{\beta}tI\right)}\left(X{t-1}\right)}=\frac{\sqrt{\tilde{\beta}_t}}{\sigma^{\prime}}
$$

而由于
$$
\int q\left(X_{t-1}|X_t,X_0\right)dx=1=\int f_{N\left(\tilde{\mu}t\left(X_t,X_0\right),\tilde{\beta}tI\right)}\left(X{t-1}\right)dx
$$
因此显然有 $\sigma^{\prime}=\sqrt{\tilde{\beta}t}$，即后验分布 $q\left(X{t-1}|X_t,X_0\right)$ 服从正态分布 $N\left(X{t-1};\tilde{\mu}_t\left(X_t,X_0\right),\tilde{\beta}_tI\right)$。

这样一来，DDPM的每一步的推断可以总结为：

1) 每个时间步通过$X_t$ 和 $t$ 来预测高斯噪声$Z_\theta\left(X_t, t\right)$，随后根据$\mu_\theta\left(X_t, t\right)=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{a}_t}} Z_\theta\left(X_t, t\right)\right)$得到均值 $\mu_\theta\left(X_t, t\right)$ .

2) 得到方差 $\Sigma_\theta\left(x_t, t\right)$ ，DDPM中使用untrained$\Sigma_\theta\left(x_t, t\right)=\tilde \beta_t$，且认为 $\tilde \beta_t = \beta_t$ 和 $\tilde \beta_t = \frac {1-\bar \alpha_{t-1}}{1-\bar \alpha_t} \cdot \beta_t$结果近似，在GLIDE中则是根据网络预测trainable方差 $\Sigma_\theta\left(x_t, t\right)$ .

3) 根据$p_\theta\left(X_{t-1} \mid X_t\right)=\mathcal{N}\left(X_{t-1} ; \mu_\theta\left(X_t, t\right), \Sigma_\theta\left(X_t, t\right)\right)$得到 $q(X_{t−1}\mid X_t)$ ，利用重参数得到$X_t−1$ .

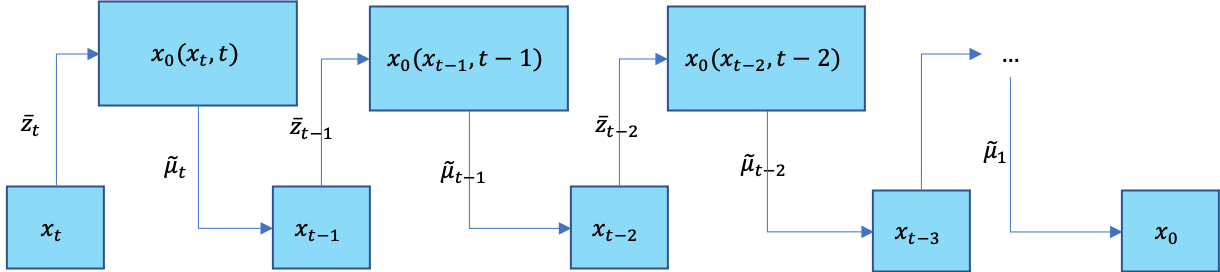
由浅入深了解Diffusion Model

Diffusion训练

现在我们假设逆扩散过程也是一个马尔可夫链过程，且有
$$
p_{\theta}\left(X_{0:\left(T-1\right)}|X_T\right)=\prod\limits_{t=1}^{T}p_{\theta}\left(X_{t-1}|X_t\right)
$$
通过对真实数据分布下，最大化模型预测分布的对数似然，即优化在 $X_0 \sim q(X_0)$ 下的 $p_\theta (X_0)$ 交叉熵：
$$
\mathcal{L}=\mathbb{E}_{q\left(X_0\right)}\left[-\log p_\theta\left(X_0\right)\right]
$$
这里我们同前面VAE一样也是计算目标数据分布的似然函数，即使用变分下限(VLB)来优化负对数似然。与前面不同的是我们这里求的是负对数的似然函数，在此基础上加上了KL散度，因为KL散度是大于等于零的，于是式子就构成了负对数似然的上界，上界越小，负对数似然也就越小，其对数似然就越大，这里也就要求KL散度越小越好，其代表的含义也就是扩散和重构过程越相似越好。

那么对于其负对数似然函数，我们有
$$
\begin{aligned}
-\log p_{\theta}\left(X_0\right)&\leq -\log p_{\theta}\left(X_0\right)+KL\left[q\left(X_{1:T}|X_{0}\right)||p_{\theta}\left(X_{1:T}|X_{0}\right)\right]\
&=-\log p_{\theta}\left(X_0\right)+E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{1:T}|X_{0}\right)}\right)\right]\
&=-\log p_{\theta}\left(X_0\right)+E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{\frac{p_{\theta}\left(X_{0:T}\right)}{p_{\theta}\left(X_{0}\right)}}\right)\right]\
&=-\log p_{\theta}\left(X_0\right)+E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]+E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(p_{\theta}\left(X_{0}\right)\right)\right]\
&=E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]\
\end{aligned}
$$

前面我们讲到所谓生成模型需要通过增大原始数据和反向过程最终生成数据的相似度来优化模型。在机器学习中，我们计算该相似度参考的是 交叉熵（ cross entropy ） 。关于交叉熵，学术上给出的定义是”用于度量两个概率分布间的差异性信息”。换句话讲，交叉熵越小，模型生成的图片就越和原始图片接近。但是，在大多数情况下，交叉熵是很难或者无法通过计算得出的，所以我们一般会通过优化一个更简单的表达式，达到同样的效果。Diffusion模型借鉴了VAE模型的优化思路，将 variational lower bound （ VLB ，又称 ELBO ）替代cross entropy来作为最大优化目标。

将对数似然转换为交叉熵，我们有
$$
\begin{aligned}
E_{x\sim q\left(X_{0}\right)}\left[-\log p_{\theta}\left(X_0\right)\right]&\leq E_{x\sim q\left(X_{0}\right)}\left{E_{x_{1:T}\sim q\left(X_{1:T}|X_{0}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]\right}\
&=E_{x\sim q\left(X_{0}\right)}\left{\int q\left(X_{1:T}|X_{0}\right)\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)dX_{1:T}\right}\
&=\int q\left(X_{0}\right)\int q\left(X_{1:T}|X_{0}\right)\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)dX_{1:T}dX_{0}\
&=\int q\left(X_{0:T}\right)\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)dX_{0:T}\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]\
\end{aligned}
$$

设 $L_{VLB}=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]$，那么要最小化交叉熵 $E_{x\sim q\left(X_{0}\right)}\left[-\log p_{\theta}\left(X_0\right)\right]$ 可以考虑直接最小化 $L_{VLB}$。继续推导 $L_{VLB}$，我们有
$$
\begin{aligned}
L_{VLB}&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{1:T}|X_{0}\right)}{p_{\theta}\left(X_{0:T}\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{\prod\limits_{t=1}^{T}q\left(X_t|X_{t-1}\right)}{p_{\theta}\left(X_T\right)\prod\limits_{t=1}^{T}p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\sum\limits_{t=1}^{T}\log\left(\frac{q\left(X_t|X_{t-1}\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_t|X_{t-1},X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_t,X_{t-1},X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)\cdot q\left(X_{t-1},X_0\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)\cdot q\left(X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)\cdot q\left(X_{t-1},X_0\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\cdot\frac{q\left(X_t|X_0\right)}{q\left(X_{t-1}|X_0\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_t|X_0\right)}{q\left(X_{t-1}|X_0\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\log\left(\frac{q\left(X_1|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)+\log\left(\frac{q\left(X_t|X_0\right)}{q\left(X_{1}|X_0\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[-\log p_{\theta}\left(X_T\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)+\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_0|X_1\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)+\sum\limits_{t=2}^{T}\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)-\log p_{\theta}\left(X_0|X_1\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)\right]+\sum\limits_{t=2}^{T}E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]-\log p_{\theta}\left(X_0|X_1\right)\
&(=\mathbb{E}q[\underbrace{D{\mathrm{KL}}\left(q\left(\mathbf{x}T \mid \mathbf{x}0\right) | p_\theta\left(\mathbf{x}T\right)\right)}{L_T}+\sum{t=2}^T \underbrace{D{\mathrm{KL}}\left(q\left(\mathbf{x}{t-1} \mid \mathbf{x}t, \mathbf{x}0\right) | p_\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right)\right)}{L{t-1}}-\underbrace{\log p_\theta\left(\mathbf{x}0 \mid \mathbf{x}1\right)}{L_0}]) \
\end{aligned}
$$
注意：$q(X_t\mid X{t-1})=q(X_t\mid X{t-1},X_0)=\frac{q(X_t,X_{t-1},X_0)}{q(X_{t-1},X_0)}=\frac{q(X_{t-1}\mid X_t,X_0)q(X_t\mid X_0)q(X_0)}{q(X_{t-1},X_0)}=\frac{q(X_{t-1}\mid X_t,X_0)q(X_t\mid X_0)}{q(X_{t-1}\mid X_0)}$

版本一

经过上面的推导，可以得到熵与多个KL散度的累加，具体可见[文献](Sohl-Dickstein, Jascha, et al. “Deep unsupervised learning using nonequilibrium thermodynamics.” International Conference on Machine Learning. PMLR, 2015.)，我们试图理解一下公式推导到最后一步后各项式子的含义：

$L_T$这一项中是不含参的，首先是其中的分母$q(X_t\mid X_0)$是仅由$\beta_t$计算而来的没有可学习参数，而$p_{\theta}(X_T)$完全是一个各项独立的高斯分布，所以$L_T$ 可以当做常量忽略。
$L_{t-1}$代表的是扩散过程中后验条件概率分布与逆扩散过程条件概率分布之间的KL散度。
$$
L_t=D_{K L}\left(q\left(X_t \mid X_{t+1}, X_0\right) | p_\theta\left(X_t \mid X_{t+1}\right)\right) ; \quad 1 \leq t \leq T-1
$$
根据多元高斯分布的KL散度求解：
$$
L_t=\mathbb{E}_q\left[\frac{1}{2\left|\Sigma_\theta\left(X_t, t\right)\right|_2^2}\left|\tilde{\mu}_t\left(X_t, X_0\right)-\mu_\theta\left(X_t, t\right)\right|^2\right]+C,
$$
其中$C$是与模型参数 $\theta$ 无关的常量。将前面$\tilde{\mu}_t\left(X_t,X_0\right)=\frac {1}{\sqrt{\alpha_t}}(X_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}\bar Z_t)$和$\mu_\theta\left(X_t, t\right)=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{a}t}} Z_\theta\left(X_t, t\right)\right)$带入上式可以得到：
$$
\begin{aligned}
L_t=& \mathbb{E}{x_0, \bar{z}_t}\left[\frac{1}{2\left|\Sigma_\theta\left(x_t, t\right)\right|_2^2}\left|\tilde{\mu}t\left(x_t, x_0\right)-\mu_\theta\left(x_t, t\right)\right|^2\right] \
=& \mathbb{E}{x_0, \bar{z}_t}\left[\frac{1}{2\left|\Sigma_\theta\left(x_t, t\right)\right|_2^2}\left|\frac{1}{\sqrt{\bar{a}_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{a}_t}} \bar{z}_t\right)-\frac{1}{\sqrt{\bar{a}_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{a}t}} z_\theta\left(x_t, t\right)\right)\right|^2\right] \
=& \mathbb{E}{x_0, \bar{z}_t}\left[\frac{\beta_t^2}{2 \alpha_t\left(1-\bar{\alpha}_t\left|\Sigma_\theta\right|_2^2\right)}\left|\bar{z}t-z_\theta\left(x_t, t\right)\right|^2\right] \
=& \mathbb{E}{x_0, \bar{z}_t}\left[\frac{\beta_t^2}{2 \alpha_t\left(1-\bar{\alpha}_t\left|\Sigma_\theta\right|_2^2\right)}\left|\bar{z}_t-z_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \bar{z}_t, t\right)\right|^2\right]
\end{aligned}
$$
从上式可以看出，diffusion训练的核心就是取学习高斯噪声$\bar z_t,z_\theta$之间的MSE。
将第三项$L_0$加入到第二项$L_{t-1}$中，两项合并就变成了$\sum_{t=1}^T {D_{{KL}}\left(q\left(\mathbf{x}{t-1} \mid \mathbf{x}_t, \mathbf{x}0\right) | p_\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}_t\right)\right)}$。

$L_0=-\log p_{\theta}\left(X_0|X_1\right)$相当于最后一步的熵，DDPM论文指出，从 $X_1$ 到 $X_0$ 应该是一个离散化过程，因为图像RGB值都是离散化的。DDPM针对$p_{\theta}\left(X_0|X_1\right)$构建了一个离散化的分段积分累乘，有点类似基于分类目标的自回归(auto-regressive)学习。

DDPM将loss进一步简化为：
$$
L_t^{\text {simple }}=\mathbb{E}_{x_0, \bar{z}_t}\left[\left|\bar{z}_t-z_\theta\left(\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\bar{\alpha}_t} \bar{z}_t, t\right)\right|^2\right]
$$
正如之前提过的，DDPM并没有将模型预测的方差$\Sigma_\theta\left(x_t, t\right)$ 考虑到训练和推断中，而是通过untrained$\beta_t$ 或者$\tilde \beta_t$代替。他们发现 $\Sigma_\theta$ 可能导致训练的不稳定。

训练过程可以看做：

1）获取输入 $X_0$，从 $1…T$ 随机采样一个 $t$ .

2) 从标准高斯分布采样一个噪声 $\bar z_t \sim N(0,I)$ .

3) 最小化$|\bar z_t - z_\theta(\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\bar{\alpha}_t} \bar{z}_t, t)|^2$ .

DDPM提供的训练/测试（采样）流程图

版本二

最后一步的 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)\right]$ 以及 $T-1$ 项 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]$ 它们并不是真正意义的KL散度，因此记
$$
\begin{aligned}
L_{VLB}&=L_T+L_{t-1}+…+L_0\
L_T&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)\right]\
L_{t-1}&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]\
L_0&=-\log p_{\theta}\left(X_0|X_1\right)\
\end{aligned}
$$

由于最后一步的 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)\right]$ 以及 $T-1$ 项 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]$ 并不是KL散度，因此我们并不能确定其优化下界是否存在，以及存在的话下界为多少，因此在讨论损失函数优化目标之前我们还需要先证明一下各个 $L_i,i=0,1,\cdots,T$ 的值的取值范围。
$$
\begin{aligned}
L_T&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_0\right)}{p_{\theta}\left(X_T\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_T|X_{0:\left(T-1\right)}\right)}{p_{\theta}\left(X_T\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{0:T}\right)}{p_{\theta}\left(X_T\right)}\right)+\log\left(\frac{1}{q\left(X_{0:\left(T-1\right)}\right)}\right)\right]\
&=KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_T\right)\right]+E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{1}{q\left(X_{0:\left(T-1\right)}\right)}\right)\right]\
\end{aligned}
$$
由于 $KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_T\right)\right]$ 和 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{1}{q\left(X_{0:\left(T-1\right)}\right)}\right)\right]$ 均大于等于0，因此 $L_T$ 大于等于0；又由于当 $q\left(X_T|X_0\right)=p_{\theta}\left(X_T\right)$ 时 $L_T$ 等于0，因此 $L_T$ 的优化下界存在且为0。
$$
\begin{aligned}
L_{t-1}&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)\right]\
&=E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{0:T}\right)}{p_{\theta}\left(X_{t-1}|X_t\right)}\right)+\log\left(\frac{q\left(X_{t-1}|X_t,X_0\right)}{q\left(X_{0:T}\right)}\right)\right]\
&=KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_{t-1}|X_t\right)\right]+E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_t|X_{t-1}\right)q\left(X_{t-1}|X_0\right)}{q\left(X_{0:T}\right)q\left(X_t|X_0\right)}\right)\right]\
&=KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_{t-1}|X_t\right)\right]+E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_t|X_{0:\left(t-1\right)}\right)q\left(X_{t-1}|X_{0:\left(t-2\right)}\right)}{q\left(X_{0:T}\right)q\left(X_t|X_{0:\left(t-1\right)}\right)}\right)\right]\
&=KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_{t-1}|X_t\right)\right]+E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{q\left(X_{0:\left(t-1\right)}\right)}{q\left(X_{0:T}\right)q\left(X_{0:\left(t-2\right)}\right)}\right)\right]\
&=KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_{t-1}|X_t\right)\right]+E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{1}{q\left(X_{t:T}|X_{0:\left(t-1\right)}\right)q\left(X_{0:\left(t-2\right)}\right)}\right)\right]\
\end{aligned}
$$
由于 $KL\left[q\left(X_{0:T}\right)||p_{\theta}\left(X_{t-1}|X_t\right)\right]$ 和 $E_{x_{0:T}\sim q\left(X_{0:T}\right)}\left[\log\left(\frac{1}{q\left(X_{t:T}|X_{0:\left(t-1\right)}\right)q\left(X_{0:\left(t-2\right)}\right)}\right)\right]$ 均大于等于0，因此 $L_{t-1}$ 大于等于0；又由于当 $q\left(X_{t-1}|X_t,X_0\right)=p_{\theta}\left(X_{t-1}|X_t\right)$ 时 $L_{t-1}$ 等于0，因此 $L_{t-1}$ 的优化下界存在且为0。
显然 $L_0$ 的优化下界存在且为0。
因此，根据上述推导过程，要最小化 $L_{VLB}$ 我们就需要最小化各个 $L_i,i=0,1,\cdots,T$，且希望模型逆扩散过程的每一步都去拟合对应的扩散过程的反向概率分布，通过对扩散过程的学习来得到逆扩散的分布，即让 $p_{\theta}\left(X_T\right)$ 学习 $q\left(X_T|X_0\right)$，让 $p_{\theta}\left(X_{t-1}|X_t\right)$ 学习 $q\left(X_{t-1}|X_t,X_0\right)$，最后让 $p_{\theta}\left(X_0|X_1\right)$ 逼近1。而又由于我们证明了 $q\left(X_T|X_0\right)$ 近似服从标准正态分布，且每一步 $q\left(X_{t-1}|X_t,X_0\right)$ 均服从正态分布，因此逆扩散过程的每一步也服从正态分布，因此我们可以假设
$$
p_{\theta}\left(X_T\right)=N\left(X_T;0,1\right)\qquad p_{\theta}\left(X_{t-1}|X_t\right)=N\left(X_{t-1};\mu_{\theta}\left(X_t,t\right),\Sigma_{\theta}\left(X_t,t\right)\right)
$$

来对生成过程进行拟合。至此，网络结构设计和损失函数设计均推导完毕。

7 结语

最后的最后，在Diffusion爆火的如今，有人也曾发出过疑问，它为什么可以做到如此的大红大紫，甚至风头开始超过GAN网络？

Diffusion的优势突出，劣势也很明显；它的诸多领域仍是空白，它的前方还是一片未知。为什么却有那么多的人在孜孜不倦地对它进行研究呢？

兴许，马毅教授的一番话，可以给我们提供一种解答。

“diffusion process的有效性以及很快取代GAN也充分说明了一个简单道理：

几行简单正确的数学推导，可以比近十年的大规模调试超参调试网络结构有效得多。“

或许，这就是Diffusion模型的魅力吧。

还有几句话也说的很有道理。

“其实与GAN一样，Diffusion也无法解决学习一般高维空间分布问题的计算复杂性问题 – 这类问题基本都是NP hard。

成功的实例固然让人高兴，但要避免过度夸大这些方法就可以解决整个这一类问题。

最后才是重点的重点：如果大家希望自己将来的成功更可把控，就好好学习几本好书把数学计算原理弄清楚；如果大家只希望靠碰运气成功，就可以继续调超参数、玩数据集。即便好不容易调出一个结果，相信我，这样的结果也很快会被最终正确的方法取代、淘汰，在历史上不留痕迹。而过了三百年，我们还会记得Laplace，他的方法还无法被取代！”

参考资料

Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising Diffusion Probabilistic Models. arXiv:2006.11239, 2020. ↩
Sohl-Dickstein J , Weiss E A , Maheswaranathan N , et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics[J]. JMLR.org, 2015. ↩
Alex Nichol & Prafulla Dhariwal. “ Improved denoising diffusion probabilistic models” arxiv Preprint arxiv:2102.09672 (2021). [code] ↩
Ling Yang, Zhilong Zhang, Shenda Hong, Runsheng Xu, Yue Zhao, Yingxia Shao, Wentao Zhang, Ming-Hsuan Yang, and Bin Cui. Diffusion models: A comprehensive survey of methods and applications. arXiv preprint arXiv:2209.00796, 2022. ↩
Ho, Jonathan, Ajay Jain, and Pieter Abbeel. “Denoising diffusion probabilistic models.” Advances in Neural Information Processing Systems 33 (2020): 6840-6851. ↩
Feller, William. “On the theory of stochastic processes, with particular reference to applications.” Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1949. ↩
Sohl-Dickstein, Jascha, et al. “Deep unsupervised learning using nonequilibrium thermodynamics.” International Conference on Machine Learning. PMLR, 2015. ↩
Sha Yuan et al. A Roadmap for Big Model ，2022. ↩
Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. ↩
邱锡鹏. 神经网络与深度学习. 机械工业出版社. https://nndl.github.io/. 2020 ↩
fish233yeah/Notes-of-Generative-Models:生成模型笔记 ↩
What are Diffusion Models? ↩
Hung-yi Lee. ML Lecture 18: Unsupervised Learning - Deep Generative Model (Part II).Youtube. 2016 ↩
deep thoughts. Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读. bilibili. 2022 ↩
AI绘画爆火背后：扩散模型原理及实现 ↩
code:Denoising Diffusion Probabilistic Model, in MindSpore ↩
由浅入深了解Diffusion Model ↩
What are Stable Diffusion Models and Why are they a Step Forward for Image Generation? ↩
Diffusion Models Made Easy ↩
diffusion model 最近在图像生成领域大红大紫，如何看待它的风头开始超过 GAN ？ ↩
生成模型(四):扩散模型 ↩
重参数化技巧：高斯分布采样 ↩
.中文版扩散模型课程：第一单元 ↩
工具人66号. 进阶详解KL散度. 知乎. 2022 ↩

学习 > Machine Learning

#生成模型 #概率模型 #VAE #扩散模型 #DDPM， Difussion Model #重参数化 #KL散度

生成模型以及扩散模型原理推导

https://blog.baixf.tk/2023/01/12/Machine Learning/生成模型以及扩散模型原理推导/

作者

白小飞

发布于

2023年1月12日

许可协议

C++ 基础知识笔记下一篇