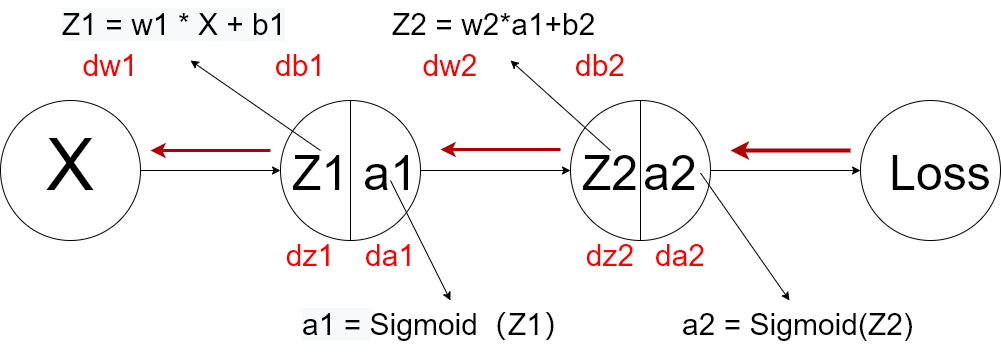
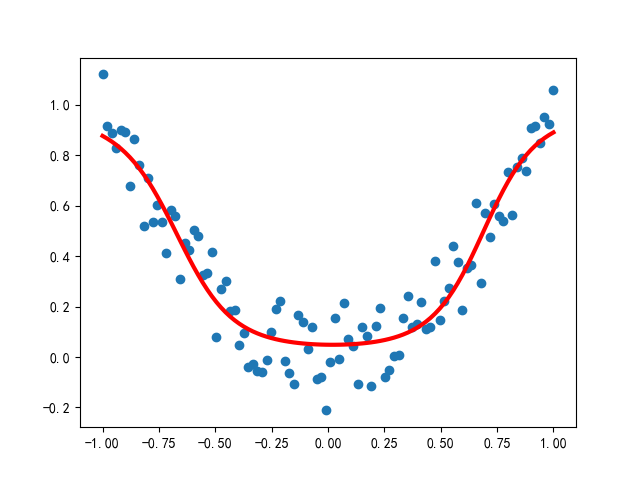
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def d_sigmoid(x):
return sigmoid(x) * (1 - sigmoid(x))
def forward(x, w1, b1, w2, b2):
z1 = np.dot(x, w1) + b1
a1 = sigmoid(z1)
z2 = np.dot(a1, w2) + b2
a2 = sigmoid(z2)
return z1, a1, z2, a2
def loss(y, a2):
return np.mean(np.square(y - a2)/2)
def backward(x, y, w1, b1, w2, b2, z1, a1, z2, a2):
dz2 = (a2 - y) * d_sigmoid(z2)
dw2 = np.dot(a1.T, dz2)
db2 = np.sum(dz2, axis=0)
da1 = np.dot(dz2, w2.T)
dz1 = da1 * d_sigmoid(z1)
dw1 = np.dot(x.T, dz1)
db1 = np.sum(dz1, axis=0)
return dw1, db1, dw2, db2
def update(w1, b1, w2, b2, dw1, db1, dw2, db2, lr):
w1 -= lr * dw1
b1 -= lr * db1
w2 -= lr * dw2
b2 -= lr * db2
return w1, b1, w2, b2
def train(x, y, w1, b1, w2, b2, lr, epoch):
for i in range(epoch):
z1, a1, z2, a2 = forward(x, w1, b1, w2, b2)
dw1, db1, dw2, db2 = backward(x, y, w1, b1, w2, b2, z1, a1, z2, a2)
w1, b1, w2, b2 = update(w1, b1, w2, b2, dw1, db1, dw2, db2, lr)
if i % 10 == 0:
print('epoch: {}, loss: {}'.format(i, loss(y, a2)))
return w1, b1, w2, b2
def predict(x, w1, b1, w2, b2):
z1, a1, z2, a2 = forward(x, w1, b1, w2, b2)
return a2
if __name__ == '__main__':
x = np.linspace(-1, 1, 100)[:, np.newaxis]
noise = np.random.normal(0, 0.1, size=x.shape)
y = np.square(x) + noise
w1 = np.random.normal(0, 1, size=(1, 10))
b1 = np.zeros(10)
w2 = np.random.normal(0, 1, size=(10, 1))
b2 = np.zeros(1)
w1, b1, w2, b2 = train(x, y, w1, b1, w2, b2, lr=0.1, epoch=1000)
y_pred = predict(x, w1, b1, w2, b2)
plt.scatter(x, y)
plt.plot(x, y_pred, 'r-', lw=3)
plt.show()
|