A2-分治思想与递归

分而治之是计算机领域中非常重要的一个思想。

一、分治法思想

分治思想主要通过递归来实现，每层递归中主要包括三个步骤：

  • 分解：即将原问题划分为若干子问题，子问题的形式要保证和原问题一致，但规模更小。

  • 解决：当划分子问题的规模足够小时，停止递归，求解子问题，获取子问题的解决结果并返回给上一层。

  • 合并：将子问题的解决结果进行合并，得到原问题的解。

也就是说，分治思想就是将一个大问题用过递归层层分解为无数个子问题，这些子问题要保证与与原问题是一个类型，只不过规模更小更加容易求解，但求解过程相同。

二、基于分治思想的排序

在排序中，将数组拆分成不同的组，此为分，每组数据分别在各自组内进行排序，此为治。分治可以很好的利用多处理器的并行计算能力，提高排序效率。今天介绍两种基于分治思想的经典排序算法：快速排序和归并排序。

1.快速排序

快速排序的基本思路是，首先选取一个基准值，然后根据基准值，将数组拆分为左右两部分，使得基准值左侧的元素，都比基准值小，右侧的元素，都比基准值大。随后，对左右两部分数组进行同样的操作：选取基准值，做划分处理。一直分到不能再分，数组就整体有序了。每经过一轮排序，该轮基准元素的位置就会被确定下来。

1、思考：如果给了我们一个无序的数组，我们该如何最快将其排序成一个有序数组？

image-20220902083852649

2、通过分治的思想，选取一个基准值，然后根据基准值，将数组拆分为左右两部分，使得基准值左侧的元素，都比基准值小，右侧的元素，都比基准值大。随后，对左右两部分数组进行同样的操作：选取基准值，做划分处理。一直分到不能再分，数组就整体有序了。每经过一轮排序，该轮基准元素的位置就会被确定下来。

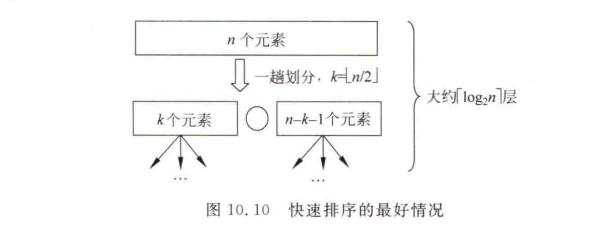
3、排序实例：为方便理解快速排序，可以建立一个快速排序递归树。以数组int[] arr = {3,23,4,13,4,5,63,6,2}为例，其快排过程及快排递归树为下图所示。

image-20220902091719408

4、性能分析

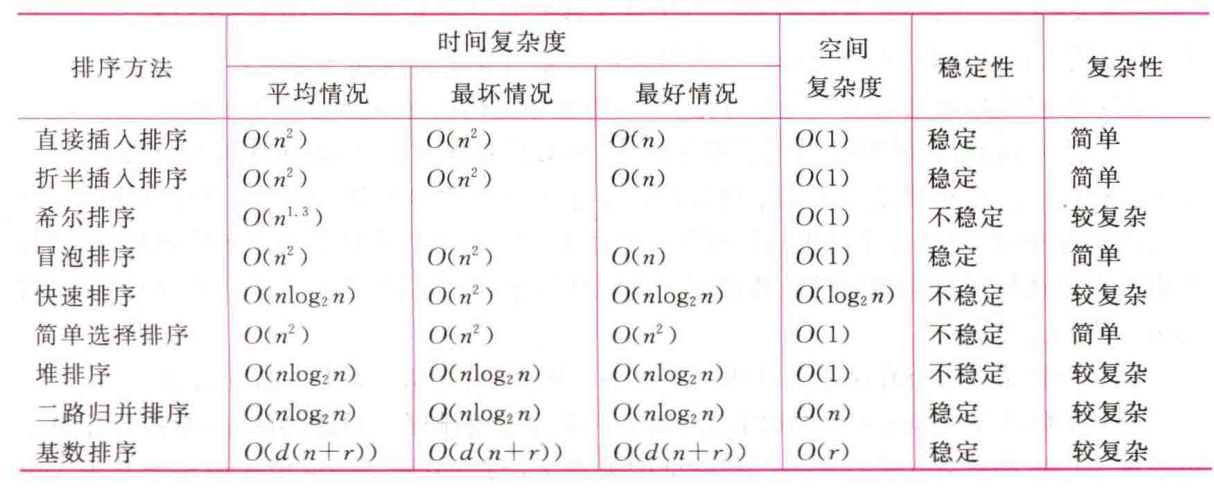
快速排序最好的情况是每一次划分都将n个元素划分成两个长度差不多的子区间，也就是说每次划分所取的基准都是当前无序区间的“中值元素”，划分的结果是基准的左右两个无序子区间的长度大致相等，如下图所示，这样的递归树高度为O(⌈logN⌉)，而在每一层划分的时间为O(N)，所以此时的时间复杂度为O(NlogN)、空间复杂度为O(logN)。快速排序最坏的情况是每一次划分选取的基准都是当前无序区间的最小值或者最大值。这样的递归树高为N，需要做N-1次划分，此时算法的时间复杂度为O(n^2)、空间复杂度为O(N)。

image-20220902093447955

image-20220902094116842

5.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//快速排序算法

int count=0;
int partition(RecType R[],int s,int t)	//一趟划分
{
	int i=s,j=t;
	RecType tmp=R[i];			//以R[i]为基准
	while (i<j)  				//从两端交替向中间扫描,直至i=j为止
	{	while (j>i && R[j].key>=tmp.key)
			j--;				//从右向左扫描,找一个小于tmp.key的R[j]
		R[i]=R[j];				//找到这样的R[j],放入R[i]处
		while (i<j && R[i].key<=tmp.key)
			i++;				//从左向右扫描,找一个大于tmp.key的R[i]
		R[j]=R[i];				//找到这样的R[i],放入R[j]处
	}
	R[i]=tmp;
	return i;
}

void QuickSort(RecType R[],int s,int t) //对R[s..t]的元素进行快速排序
{	int i;
	RecType tmp;
	if (s<t) 					//区间内至少存在两个元素的情况
	{	count++;
		i=partition(R,s,t);
		DispList(R,10);			//调试用
		QuickSort(R,s,i-1);		//对左区间递归排序
		QuickSort(R,i+1,t);		//对右区间递归排序
	}
}

2.归并排序

归并排序是一种建立在归并操作上的排序算法，它是典型的分而治之思想的体现。其基本思路是，先对待排序数组进行分区，比如一个大小为8的数组，先对它进行分区，一分为二，二分为四，四分为八，当已经分到不能再分（分区只有一个元素），我们可以认为这个分区是有序的。随后便可以对分区进行两两合并。随后，每个分区变为了2个元素，且各个分区内部都是有序的，我们便可以对相邻分区再次进行两两合并，随后，每个分区变为了4个元素，且各个分区内部都是有序的，再次对相邻分区进行合并，只有1个分区，排序结束，数组整体有序。

1、思考：如果给了我们两个已经做好排序的数组（相同排序规则）A和B，我们该如何将其合并到一个有序数组C？

这个问题很简单，依次从两个数组中取元素比较然后放进C中即可。而如果A、B数组都只有一个元素时，他们都成为了一个有序数组，则可以直接进行比较放在数组C中，返回有序的数组C。

2、通过分治思想对无序数组排序问题进行划分：对于一个无序的数组array

（1）分解：通过递归将无序数组进行划分，每次从array.length/2处划分为两个数组，直到划分后的子数组规模为1。

（2）解决：当子数组规模为1时，此时的最小规模数组已经自动变为一个有序数组，递归终止返回有序数组结果。

（3）合并：接收下一层递归所返回的两个有序子数组，将这两个有序子数组的数据进行合并为一个新的有序数组，然后返回该有序数组给上一层递归。

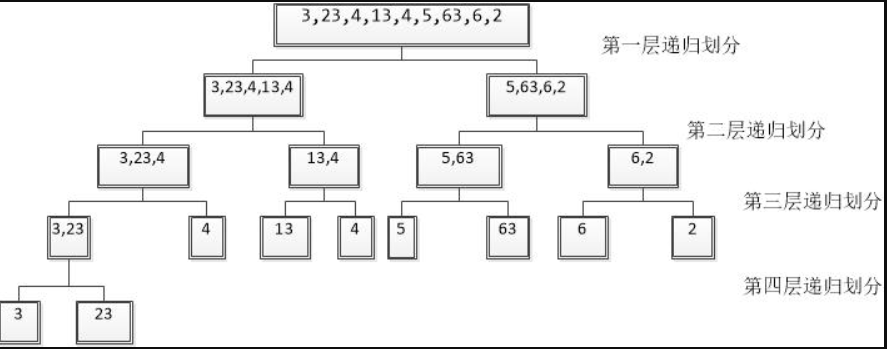
3、排序实例：为方便理解递归划分数组，可以建立一个递归树形图（理解递归比较方便）。以数组int[] arr = {3,23,4,13,4,5,63,6,2}为例，其数组划分树形图为

image-20220902094237595

4.性能分析

对于长度为N的排序表，二路归并需要进行⌈logN⌉趟，每趟归并时间为O(N)，故其时间复杂度无论在最好还是最还情况下都是O(N⌈logN⌉)，显然平均时间复杂度也是O(N⌈logN⌉)。

在二路归并排序的过程中，每次二路归并都需要使用一个辅助数组来暂存两个有序子表归并的结果，而每次二路归并后都会释放其空间，但最后一趟需要所有元素参与归并，所以总的辅助空间复杂度为O(N)。

5.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//自底向上的二路归并排序算法
#include <malloc.h>
#include "seqlist.cpp"

void Merge(RecType R[],int low,int mid,int high) 
{
	RecType *R1;
	int i=low,j=mid+1,k=0; //k是R1的下标,i、j分别为第1、2段的下标
	R1=(RecType *)malloc((high-low+1)*sizeof(RecType));  //动态分配空间
	while (i<=mid && j<=high)     	//在第1段和第2段均未扫描完时循环
		if (R[i].key<=R[j].key)    	//将第1段中的记录放入R1中
		{
			R1[k]=R[i];
			i++;k++; 
		}
		else                       		//将第2段中的记录放入R1中
		{
			R1[k]=R[j];
			j++;k++; 
		}
	while (i<=mid)          	       	//将第1段余下部分复制到R1
	{ 
		R1[k]=R[i];
		i++;k++; 
	}
    while (j<=high)                	//将第2段余下部分复制到R1
	{
		R1[k]=R[j];
		j++;k++;  
	}
    for (k=0,i=low;i<=high;k++,i++) //将R1复制回R中
	    R[i]=R1[k];
} 
void MergePass(RecType R[],int length,int n)	//对整个数序进行一趟归并
{
	int i;
	for (i=0;i+2*length-1<n;i=i+2*length) 	//归并length长的两相邻子表
		Merge(R,i,i+length-1,i+2*length-1);
	if (i+length-1<n-1)                		//余下两个子表,后者长度小于length
		Merge(R,i,i+length-1,n-1);  		//归并这两个子表
	printf("length=%d: ",length);
	DispList(R,n);
}
void MergeSort(RecType R[],int n)			//自底向上的二路归并算法
{
	int length;
	for (length=1;length<n;length=2*length)//进行log2n趟归并
		MergePass(R,length,n);
}

三、基于分治思想的查找

1.折半查找/二分查找

折半查找法，是一种常用的查找方法，该方法通过不断缩小一半查找的范围，直到达到目的，所以效率比较高。

1.折半查找的基本思想

首先将给定值key与表中中间位置的元素比较，若相等，则查找成功，返回该元素的存储位置；若不等，则所需查找的元素只能在中间元素以外的前半部分或后半部分(例如，在查找表升序排列时，若给定值key大于中间元素，则所查找的元素只可能在后半部分)。然后在缩小的范围内继续进行同样的查找，如此重复，直到找到为止，或确定表中没有所需要查找的元素，则查找不成功，返回查找失败的信息。

2.例如，已知11个元素的有序表{7, 10, 13, 16, 19, 29, 32, 33,37,41,43}，要查找值为11，我们可以画出折半查找判定树。

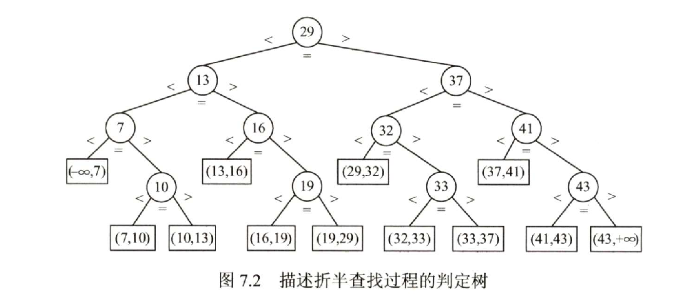
image-20220904003906103

若有序序列有N个元素，则对应的判定树有N个圆形的非叶结点和N+1个方形的叶结点。显然，判定树是一棵平衡二叉树。同样我们也可以理解为，N个隔板把(-∞,+∞)分成了N+1个失败情况区间。

3.复杂度及适用性。

针对有序数组（元素从小到大或从大到小），由上述分析可知，用折半查找法查找到给定值的比较次数最多不会超过树的高度，折半查找的判定树中，只有最下面一层是不满的。因此，元素个数为n时树高h = ⌈log2(n + 1)⌉。所以优点是查找速度比较快，时间复杂度为O(logN)，平均情况下比顺序查找的效率高。

4.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//折半查找算法

int BinSearch(RecType R[],int n,KeyType k) //折半查找算法
{	int low=0,high=n-1,mid;
	while (low<=high)			//当前区间存在元素时循环
	{	mid=(low+high)/2;
		if (k==R[mid].key)		//查找成功返回其逻辑序号mid+1
			return mid+1;
		if (k<R[mid].key)		//继续在R[low..mid-1]中查找
			high=mid-1;
		else					//k>R[mid].key
			low=mid+1;			//继续在R[mid+1..high]中查找
	}
	return 0;					//未找到时返回0（查找失败）
}

四、递归与分治之间的关系

递归可以用来写分治，也可以用来写别的，比如 DFS、树的遍历之类的。

分治可以用递归写，也可以不用递归写，比如用个队列加循环也能完成，就是麻烦点。

递归和分治是两个不同维度的概念。递归是程序的的实现方式，自己调用自己。而分治是一种算法（解决问题的方法），本质是把问题拆分。

递归用于解决什么样的问题：

1）各种数学问题：8皇后问题，汉诺塔，阶乘问题，迷宫问题，球和篮子问题等；（回溯，如果不能则会返回继续寻找）

2）各种算法中，例如快速排序，归并排序，二分查找，分治算法等；

3）将用栈解决的问题，利用递归代码会更加简洁。

参考

  1. 李春葆. 数据结构与算法教程[M]. 清华大学出版社, 2005. ↩
  2. 2023年王道考研数据结构复习指导[M]. 中国工信出版集团. ↩
  3. 排序算法——分治思想与归并排序 ↩
  4. 分治思想——快速排序算法 ↩
  5. 折半查找的算法思想、实现及其判定树的查找和构造（C语言） ↩
  6. 递归和分治思想（折半查找） ↩
  7. 递归和分治有什么区别吗？ ↩
学习 > Data Structure
#排序 #查找 #分治 #递归
A2-分治思想与递归
https://blog.baixf.tk/2022/09/03/Data Structure/A2-分治思想与递归/
作者
白小飞
发布于
2022年9月3日
许可协议