Q2-数据结构

题目1

(摘自王道考研数据结构7.3.4习题第二十二题)

在任意一颗非空二叉树排序树中T1中，删除某结点v之后形成二叉排序树T2，再将v插入T2形成二叉排序树T3.

关于T1与T3， ①若v是T1的叶结点，则T1与T3一定相同，②若v不是T1的叶结点，则T1与T3一定不同

分析

其实二叉排序树很好理解，如果删除的是一个叶子节点，那么删除后再插入得到的树肯定和原来删除前的树一样；针对非叶子节点，因为我们知道二叉排序树每次插入其本质是查找到一个叶子位置，然后往叶子节点上插，所以插入后得到的树肯定和原来删除前的树不一样。

题目2

(摘自王道考研数据结构7.3.4习题第二十六题)

在任意一棵非空平衡二叉树（AVL 树）T1 中，删除某结点 v 之后形成平衡二叉树 T2，再将 v 插入 T2 形成平衡二叉树 T3。

关于 T1 与 T3 ，① 无论 v 是 T1 的叶还是非叶子结点，则 T1 与 T3 可能相同也可能不相同

分析

针对叶子节点，删除前和删除后一样咱们可以很容举出例子来；针对叶子节点删除前后不同的情况，咱们不妨想一下，如果删除后导致了树的不平衡，势必会导致树的调整，以至于导致再插入删除的节点后树的状态和删除前的状态不一样。

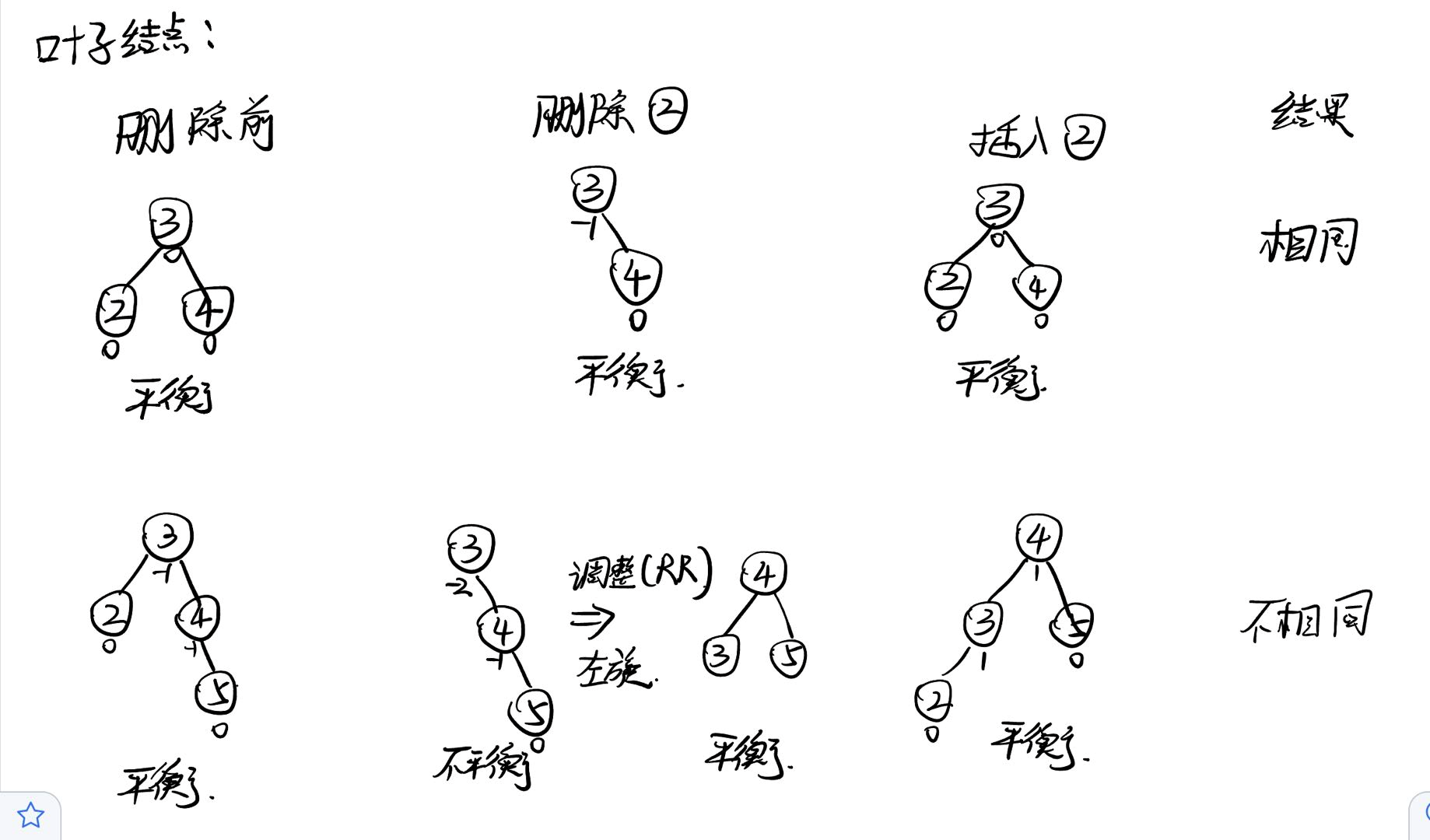
针对非叶子节点，这里就比较难想了，因为我们知道平衡二叉树是一种特殊的二叉排序树，所以针对非叶子节点，删除前和删除后二叉排序树都一定不一样了，作为一种特殊的二叉排序树所以平衡二叉树肯定存在插入与删除前不同的情况；至于相同的就不太好想了。

4、在任意一棵非空平衡二叉树（AVL 树）T1 中，删除某结点 v 之后形成平衡二叉树 T2，再将 v 插入 T2 形成平衡二叉树 T3。下列关于 T1 与 T3 的叙述中，正确的是（）。

I．若 v 是 T1 的叶结点，则 T1 与 T3 可能不相同
II．若 v 不是 T1 的叶结点，则 T1 与 T3 一定不相同
III．若 v 不是 T1 的叶结点，则 T1 与 T3 一定相同

A、仅 I
B、仅 II
C、仅 I、II
D、仅 I、III

答案：A

解析：在非空平衡二叉树中插入结点，在失去平衡调整前，一定插入在叶结点的位置。
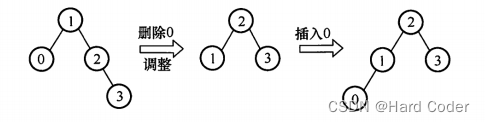
若删除的是T1的叶结点，则删除后平衡二叉树不会失去平衡，即不会发生调整，再插入此结点得到的二叉平衡树T1与T3相同;若删除后平衡二叉树失去平衡而发生调整,再插入结点得到的二叉平衡树T3与T1可能不同。I正确。例如，如下图所示，删除结点0，平衡二叉树失衡调整，再插入结点0后，平衡二叉树和以前不同。
对于比较绝对的说法II和III，通常只需举出反例即可。

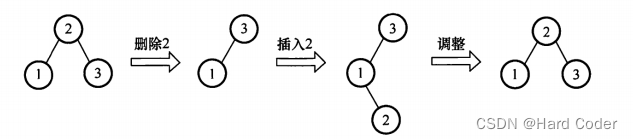
若删除的是T1的非叶结点，且删除和插入操作均没有导致平衡二叉树的调整(这时可以首先想到删除的结点只有一个孩子的情况)，则该结点从非叶结点变成了叶结点，T1与T3显然不同。例如，如下图所示，删除结点2,用右孩子结点3填补，再插入结点2，平衡二叉树和以前不同。

若删除的是T1的非叶结点，且删除和插入操作后导致了平衡二叉树的调整，则该结点有可能通过旋转后继续变成非叶结点，T1与T3相同。例如，如下图所示，删除结点2,用右孩子结点3填补，再插入结点2，平衡二叉树失衡调整，调整后的平衡二叉树和以前相同。