答疑与总结-李宏毅机器学习
一、问题
1.为什么要做深度学习而不是宽度学习?
2.为什么说最小交叉熵就是最大似然估计?
3.特征缩放和特征标准化有什么区别呢?
可以认为Feature Scaling包括Standardization和Normalization,其中Standardization可以叫做Z-Score Normalization。
二、思维导图
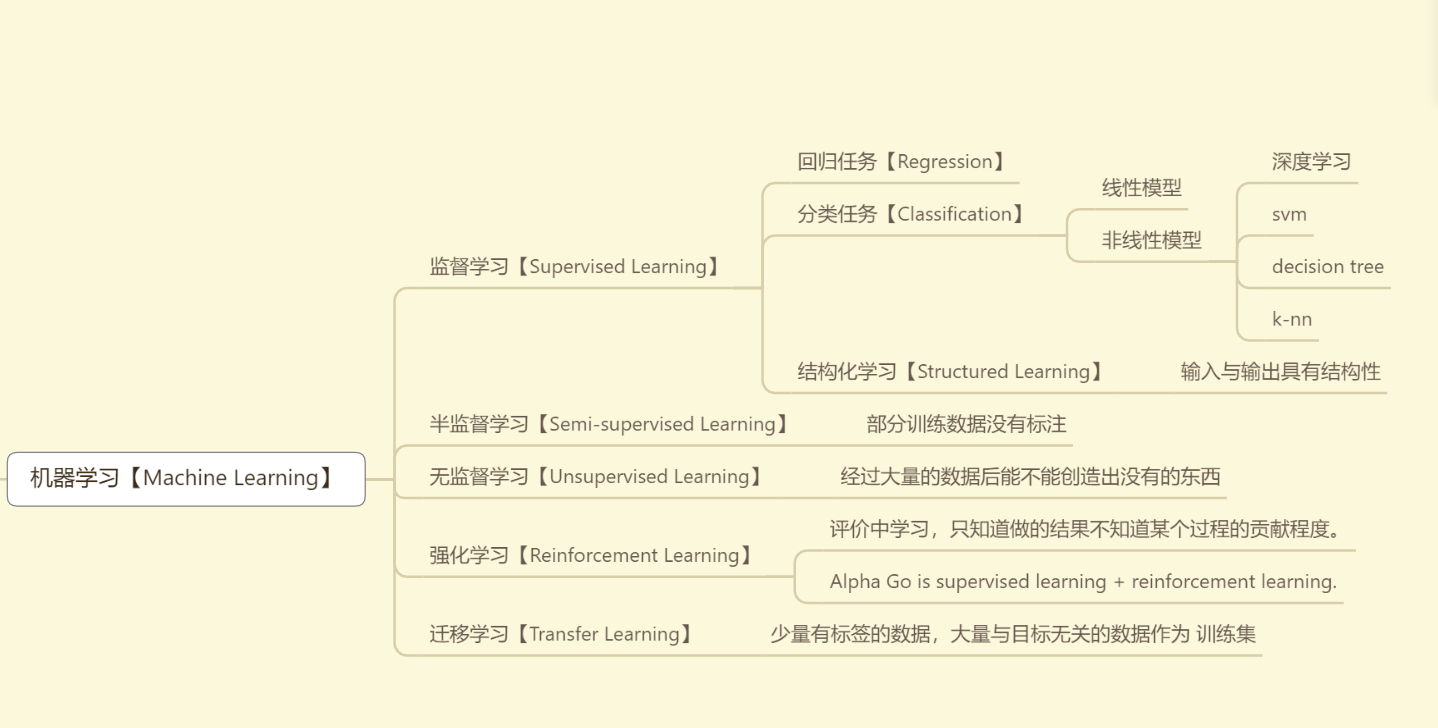
机器学习【Machine Learning】
监督学习【Supervised Learning】
回归任务【Regression】
分类任务【Classification】
线性模型
非线性模型
深度学习
svm
decision tree
k-nn
结构化学习【Structured Learning】
- 输入与输出具有结构性
半监督学习【Semi-supervised Learning】
- 部分训练数据没有标注
无监督学习【Unsupervised Learning】
- 经过大量的数据后能不能创造出没有的东西
强化学习【Reinforcement Learning】
评价中学习,只知道做的结果不知道某个过程的贡献程度。
Alpha Go is supervised learning + reinforcement learning.
迁移学习【Transfer Learning】
- 少量有标签的数据,大量与目标无关的数据作为 训练集
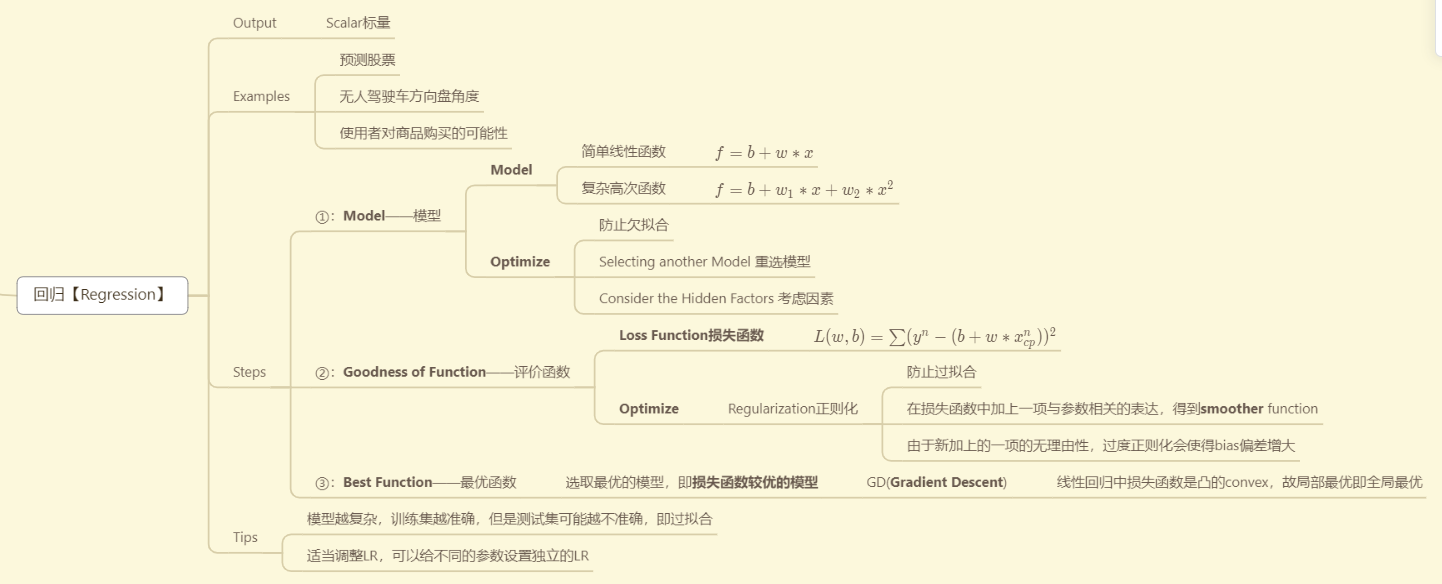
回归【Regression】
Output
- Scalar标量
Examples
预测股票
无人驾驶车方向盘角度
使用者对商品购买的可能性
Steps
①:Model——模型
Model
简单线性函数
- f=b+w∗xf=b+w*xf=b+w∗x
复杂高次函数
- f=b+w1∗x+w2∗x2f=b+w_{1}*x+w_{2}*x^{2}f=b+w1∗x+w2∗x2
Optimize
防止欠拟合
Selecting another Model 重选模型
Consider the Hidden Factors 考虑因素
②:Goodness of Function——评价函数
Loss Function损失函数
- L(w,b)=∑(yn−(b+w∗xcpn))2L(w,b)=\sum(y^{n}-(b+w*x_{cp}^{n}))^{2}L(w,b)=∑(yn−(b+w∗xcpn))2
Optimize
Regularization正则化
防止过拟合
在损失函数中加上一项与参数相关的表达,得到smoother function
由于新加上的一项的无理由性,过度正则化会使得bias偏差增大
③:Best Function——最优函数
- 选取最优的模型,即损失函数较优的模型
- GD(Gradient Descent)
- 线性回归中损失函数是凸的convex,故局部最优即全局最优
- GD(Gradient Descent)
- 选取最优的模型,即损失函数较优的模型
Tips
模型越复杂,训练集越准确,但是测试集可能越不准确,即过拟合
适当调整LR,可以给不同的参数设置独立的LR
误差【Error】
from
偏差【bias】
方差【variance】
【Error】 =【 Bias】 +【Variance】
以打靶为例,偏差就是偏离靶心的程度,方差就是离散程度
Estimator
Bias
无偏估计(Unbiased)
E[m]=E[1N∑xn]=1N∑E[xn]=uE[m]=E[\frac{1}{N}\sum{x^{n}}]=\frac{1}{N}\sum{E[x^{n}]}=uE[m]=E[N1∑xn]=N1∑E[xn]=u
Variance
取决于样本数量
有偏估计(Biased)
E[s2]=N−1Nσ2E[s^{2}]=\frac{N-1}{N}\sigma^{2}E[s2]=NN−1σ2
deal
偏差大
欠拟合
没有很好的训练
选择复杂模型,考虑其他因子
方差大
过拟合
很好训练但测试集错误很大
增加数据、正则化、数据增强
model selection
一般需要在两种误差中做权衡,通常是采用交叉验证法使得总误差最小
交叉验证法
验证集方法
- 随机平分训练集为训练集与验证集
K-折交叉验证
- 训练集分为KKK份,选取111份作为验证集,其余作为训练集,重复KKK轮,取最终的平均值为得分
Tips
- 为什么有很多的模型
- 同一模型在不同的训练集找到的f∗f^{*}f∗不同
- 为什么有很多的模型

梯度下降【Gradient descent】
define
一种寻找目标函数最小化的方法
沿梯度下降的方向求解极小值(也可以沿梯度上升方向求解极大值)
数学理论
- 对损失函数作泰勒展开
limited
容易陷入局部极值
可能卡在非极值
微分值为0
微分值小于某一个数值,约等于0
Tips
学习率【Learning Rate】
意义
监督学习以及深度学习中重要的超参
决定着目标函数能否收敛到局部最小值以及何时收敛到最小值
合适的学习率能够使目标函数在合适的时间内收敛到局部最小值
调整方法
手动调整
将参数改变对损失函数的影响进行可视化。
学习率太小,损失函数下降的非常慢;
学习率太大,损失函数下降很快,但马上就卡住不下降了;
学习率特别大,损失函数就飞出去了;
自适应学习率
随着次数的增加,通过一些因子来减少学习率
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
Adagrad算法
- 每个参数的学习率都把它除上之前微分的均方根。
随机梯度下降法
使得训练更快
损失函数不需要处理训练集所有的数据,只需要计算某一个例子的损失函数Ln,就可以赶紧update 梯度
特征缩放
两个输入的分布的范围很不一样,将他们的范围缩放,使得不同输入的范围是一样的。
使不同的特征具有相同的范围
结果是参数更新比较有效率
方法
- 归一化

深度学习【Deep Learning】
Ups and downs
1958: Perceptron (linear model)
1969: Perceptron has limitation
1980s: Multi-layer perceptron
- Do not have significant difference from DNN today
1986: Backpropagation
- Usually more than 3 hidden layers is not helpful
1989: 1 hidden layer is “good enough”, why deep?
2006: RBM initialization (breakthrough)
2009: GPU
- 【09年的GPU的发展是很关键的,使用GPU矩阵运算节省了很多时间】
2011: Start to be popular in speech recognition
2012: win ILSVRC image competition
- 感知机(Perceptron)非常像我们的逻辑回归(Logistics Regression)只不过是没有sigmoid激活函数。
Steps
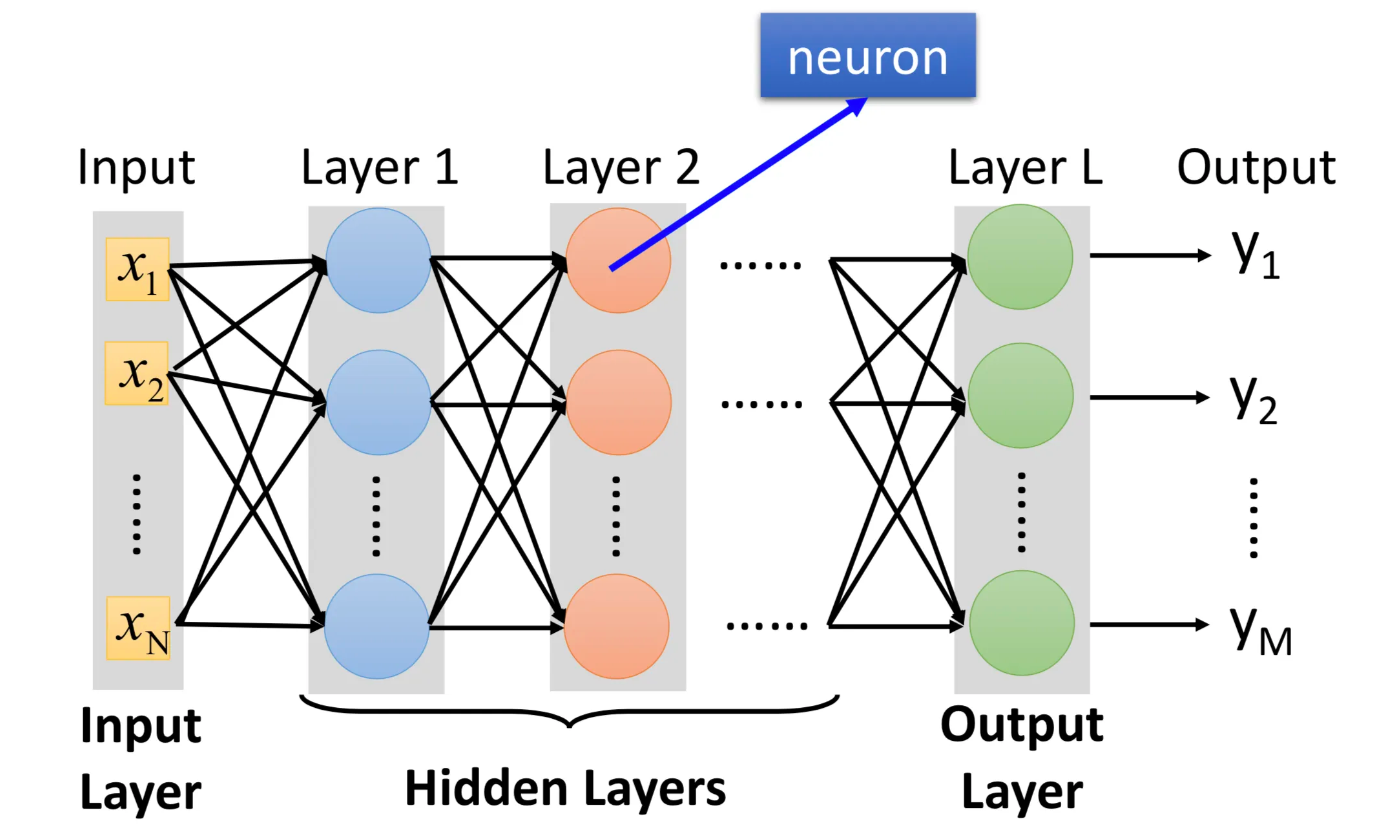
Step1:神经网络【Neural network】
组成
神经网络由若干 神经元 连接构成
神经元neuronneuronneuron为一些逻辑回归函数
参数【network parameter θ\thetaθ 】
- 所有neuronneuronneuron 的权重以及偏差就是network的parameter参数
一般结构
输入层(1)
隐藏层(N)
输出层(1)
连接方式【connection】
采用不同的connection得到不同的network structures
神经网络的结构决定了函数集(function set),因此网络结构(network structured)很关键。
connection可以自己动手设计
比如卷积神经网络【CNN】
全连接前馈神经网络【Full Connect Feedforward Network】
全连接
- 相邻两层都有连接
前馈
- 传递方向从后往前传
自动找到神经网络的结构的
- 进化人工神经网络,并不普及
Step2:模型评价【Goodness of function】
- 损失函数
- 交叉熵【cross entropy】函数计算yyy与y^\hat{y}y^的损失,调整参数使得交叉熵最小
- 损失函数
Step3:选择最优【Pick best function】
梯度下降【Gradient Descent】
反向传播【Backpropagation】
内容
正向传播过程
- 输入信息通过逐层处理并传向输出层。
反向传播过程
如果在输出层得不到期望的输出值,则通过构造输出值与真实值的损失函数作为目标函数,转入反向传播。
逐层求出目标函数对各神经元权值的偏导数,构成目标函数对权值向量的梯度,作为修改权值的依据,网络的学习在权值修改过程中完成。
输出值与真实值的误差达到所期望值时,网络学习结束。
Tips
建立在梯度下降法的基础
适合于多层神经元网络
神经网络中计算损失最好的方法,可用框架来进行计算损失【TensorFlow、theano、Pytorch】
Tips
1.为什么要用深度学习,深层架构带来哪些好处?那是不是隐藏层越多越好?
层次越深效果越好
普遍性定理
- 对于任何一个连续的函数,都可以用足够多的隐藏层来表示。
2.深度学习(Deep Learning)能表达出以前所不能表达的情况。
3.Deep的含义:许多隐藏层
4.层层之间是矩阵运算【Matrix Operation】
- 可以采用GPU矩阵加速计算
5.本质:通过隐藏层进行特征转换
6.需要不断试错以及直觉确定层数以及 神经元个数
7.损失函数
损失函数(Loss function)是定义在单个训练样本上的,也就是就算一个样本的误差,比如我们想要分类,就是预测的类别和实际类别的区别,是一个样本的,用L表示。
代价函数(Cost function)是定义在整个训练集上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和的平均,有没有这个平均其实不会影响最后的参数的求解结果。
总体损失函数(Total loss function)是定义在整个训练集上面的,也就是所有样本的误差的总和。也就是平时我们反向传播需要最小化的值。

卷积神经网络【CNN】
Why CNN
- 普通神经网络需要太多的参数,减少输入的参数,简化神经网络
CNN in image
image
少数的pattern 就能代表whole image,不需要去看整个image去识别
pattern 出现在不同区域但是表示相同的意义
图片下采样subsampling不会改变目标
CNN架构
input
convolution
- patterns处理
max pooling
- 图片下采样subsampling
flattern
- 将feature map拉直后作为feedforward netwwork的输入
fully connected feedforward network
convolution vs fully connected
- convolution就是fully connected拿掉一些weight的结果
CNN in Keras
- 唯一要改的是:network structure和input format,向量改为3维张量
CNN learned
- 每一个filter所做的事情就是detain不同角度的线条
Deep Dream
如果你给machine一张image,它会在这张image里加上它看到的东西
应用
- 图片风格迁徙
application
围棋
语音
文本

网络设计技巧
如果optimization失败了
现象
参数在更新,loss在下降,但是不满意
一开始loss就掉不下去
失败的原因一——微分为000
gradient is close to 0 【原因】
critical point
内容
local minima
saddle point 鞍点
类型判断【判断黑塞矩阵H的特征值】
原理
- 要知道loss function的形状
- 给定某一组参数,就可以写出参数附近的损失函数
原理:泰勒级数展开
- 给定某一组参数,就可以写出参数附近的损失函数
- 要知道loss function的形状
结论
都大于0则为local minima
都小于0则为local maxima
有正有负则为saddle point
- H给出了参数更新方向,新的参数为特征向量加上此时参数
【实际上不是这样处理的,还有更加优秀的处理鞍点的方法】
- H给出了参数更新方向,新的参数为特征向量加上此时参数
常见程度
维度越高,local minima越少,local minima 是比较不常见的
saddle point 鞍点更加常见
Batch and Momentum【解决方案】
Batch
原因
实际上算微分的时候,不是对所有的data算出来的L做微分
把所有的data分成一个一个的batch,从第一个batch开始计算,由上一个计算下一个L的参数
会用到shuffle
为什么要用batch
比较
batch带来的帮助
- small batch size help escape critical point
momentum
作用
有可能对抗critical point 的技术
momentum help escape critical point
原理
- 即使gradient为0,由于动量依旧可以往前动一点点,从而跳出critical point
下一步方向
- 综合考虑gradient和之前的移动决定下一步的方向
失败的原因二——学习率
现象
- loss不再下降,而梯度范数在不断的变换
自动调整学习速率【Adaptive Learning Rate】
内容
- 之前的gradient设置的同样的learning rate,启发想到给不同的参数设置不同的学习率
大原则
如果在某一个方向上,gradient 的值很小,非常的平坦,我们希望learning rate 调大一点
如果在某一个方向上,gradient 的值很大,非常的陡峭,我们希望learning rate 调小一点
更新方式
引入root mean square均方根
应用
Adagrad
RMSProp方法【Adagrad的改进】
- Adam:RMSProp+Momentum
tips
- 由于只考虑大小,所以可以和Momentum叠加使用
问题
内容
- 由于使用了之前的gradient,累积了很多σ\sigmaσ导致后面会不时走到很大的地方
Learning Rate Scheduling【解决方案】
原理:使得lr和时间有关
Learning Rate Decay
- 随着训练发生,我们越来越接近目的,所以我们减小学习率
Warm up
学习率先变大后变小
Residual Network残差网络
RAdam
失败的原因三——损失函数
- 损失函数也可能有影响
- 在分类中,损失函数采取 MSEMSEMSE 和 Cross−entopyCross-entopyCross−entopy 的结果不一样
- 损失函数也可能有影响
设计技巧——批标准化
适用场景
- 想要“铲平”凹凸部分,改变error surface
简介
批标准化(Batch Normalization,BN),又叫批量归一化,是一种用于改善人工神经网络的性能和稳定性的技术。 这是一种为神经网络中的任何层提供零均值/单位方差输入的技术。
它用于通过调整和缩放激活来规范化输入层。
优点
减少了参数的人为选择,可以取消dropout和L2正则项参数,或者采取更小的L2正则项约束参数。
减少了对学习率的要求。
可以不再使用局部响应归一化了,BN本身就是归一化网络(局部响应归一化-AlexNet)。
更破坏原来的数据分布,一定程度上缓解过拟合。
