Class4 隐马尔科夫模型HMM

一、隐马尔可夫模型的基本概念

隐马尔可夫模型：Hidden Markov Model (HMM)

定义

• 隐马尔可夫模型是关于时间序列的概率模型
• 描述由一个隐藏的马尔可夫链随机生成不可观测的状态序列(state sequence)，再由各个状态生成一个

观测而产生观测序列(observation sequence)的过程，序列的每一个位置又可以看作是一个时刻。

组成

HMM由初始概率分布、状态转移概率分布和观测概率分布决定，当观测为离散值时：

HMM的两个基本假设

• 齐次马尔可夫性假设：隐藏的马尔可夫链在时刻𝑡的状态只和𝑡 − 1的状态有关
  
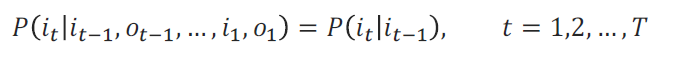
• 观测独立性假设：观测只和当前时刻的状态有关
  

隐马尔可夫模型的基本概念：生成过程

隐马尔可夫模型的三个基本问题

二、隐马尔可夫模型的三个基本问题

概率计算问题

直接计算法

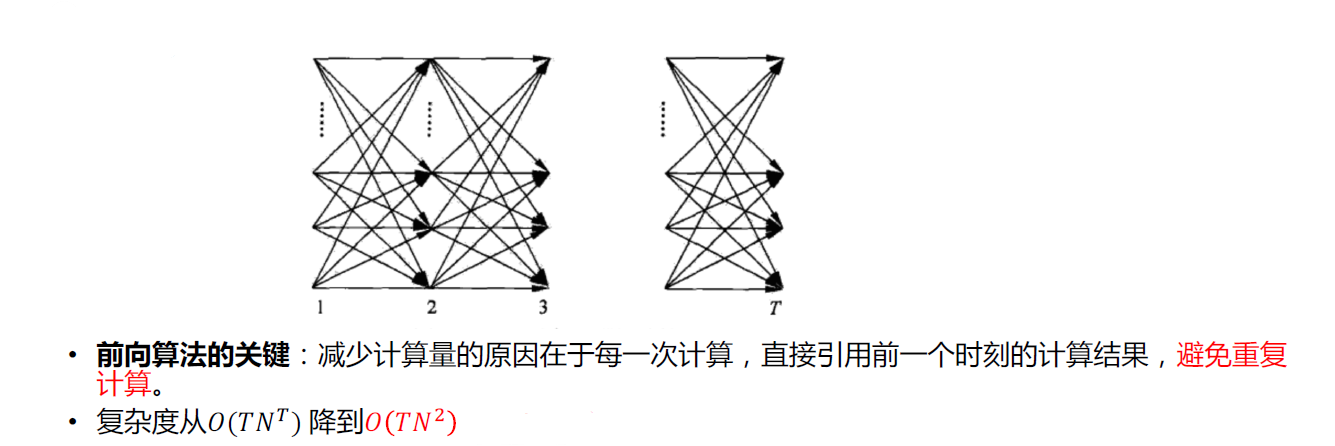
前向算法（Forward Algorithm）

找出从时刻1 → . . . → t → . . . → T ，前向概率的递归关系。

后向算法（Backward Algorithm）

找出从时刻T → . . . → t → . . . → T ，后向概率的递归关系。

预测问题

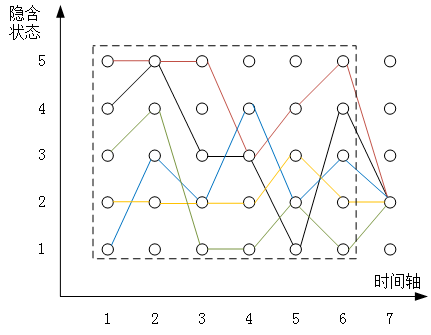
Viterbi算法

学习问题

Viterbi学习算法

• 如果已知状态-观测对齐序列，每个观测o_t对应一个具体的状态
• 状态-观测对齐序列可通过Viterbi解码算法得到，也可通过人工标注得到（代价昂贵）
• 𝜋_i 可通过最大似然估计得到（数数）
• 𝑎_ij 也可通过最大似然估计得到（数数）
• 可得到每个状态 𝑗 对应的观测集合 𝑍_j= 𝑦3, 𝑦4,…, 𝑦6
• 每个状态对应一个GMM，也就得到了每个GMM对应的观测集合 𝑍_j= 𝑦3, 𝑦4,…, 𝑦6

Baum-Welch学习算法

Baum-Welch算法可以解决无监督学习的隐马尔可夫问题，也就是说，如果我们现在有一个训练集没有状态序列，只有观测序列，我们可以使用baum-welch算法求隐马尔科夫模型参数。

参考

1. HMM的基本概念 ↩
2. HMM的概率计算问题 ↩
3. 如何通俗地讲解 viterbi 算法？ ↩