Class3 GMM以及EM算法
2022.07.14 写在前面,希望以后随着不断理解不要打脸:个人感觉EM算法本质上就是一个神经网络模型设计的思想,而GMM、K-means无非就是EM算法的一个实际应用;以GMM为例,E步是来计算后验概率的,可类比与损失函数的计算;而M步呢,对于GMM来说是重新估计参数的,而神经网络模型设计上相应的就是权值的优化。
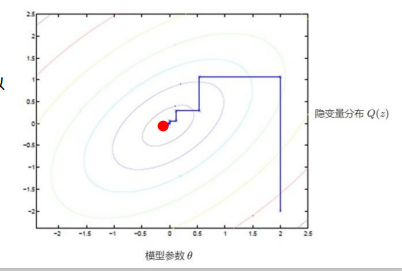
一、潜变量模型
观测模型(observed variable)
- 直接可以观测到的变量
潜(隐)变量(latent variable)
- 无法直接被观测到,需要通过模型和观测变量进行推断
- 利用潜变量来解释观测变量的数学模型,称为潜变量模型, GMM、HMM都是潜变量模型
- 潜变量模型将不完全数据(只有观测数据)的边缘分布转换成容 易处理的完全数据(观测数据+潜变量)的联合分布
eg:潜变量是类别,是未知的;观测变量是数据点,通过观测变量,推断出属于同一个类别的观测变量;
二、K-Means聚类
1.定义
k-means 算法是一种基于划分的聚类算法,它以 k 为参数,把 n 个数据对象分成 k 个簇,使簇内具有较高的相似度,而簇间的相似度较低。(P.S:K值已经给出)
2.K-means思路
- 从样本中选择 K 个点作为初始质心(随机),对应为引入K个D维均值向量为聚类中心
- 计算每个样本到各个质心的距离(如欧氏距离),将样本划分到距离最近的质心所对应的簇中
- 根据新的聚类结果计算每个簇内所有样本的均值,并使用该均值更新簇的聚类中心
- 重复步骤 2 与 3 ,直到满足一定的停止准则
停止准则:聚类中心变动不大,每个数据点所属的类别不再变化时即可停止
3.引入隐变量

4.模型优化:两阶段迭代优化方法

5.K-means聚类应用
图像分割和压缩,eg: k=2时只需要保存两种颜色即可

三、GMM模型
高斯混合模型の目标就是将不完整数据的边缘分布转换为完全数据的联合分布。
- 高斯分布
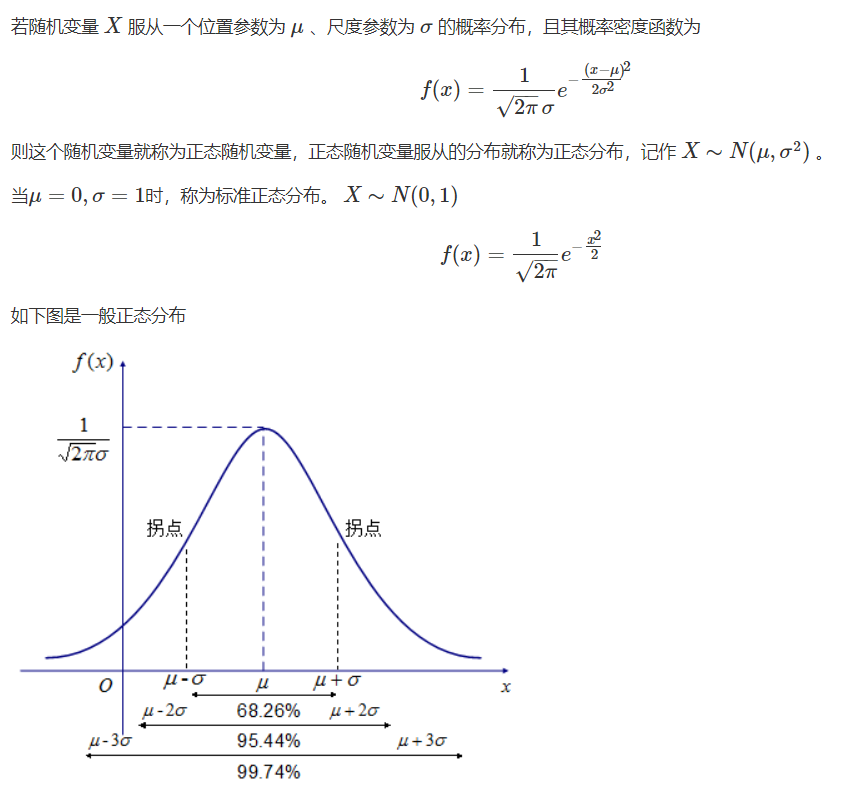

为什么选择高斯分布
高斯分布在自然界的数据中广泛存在,具有一些很好的数学性质,比如多个高斯分布的乘积可以形成另一个高斯分布
描述高斯分布只需要 2 个参数,它们就是该分布的本质信息,同也容易计算和解释。
中心极限定理:在适当的条件下,大量相互独立随机变量的均值经适 当标准化后依分布收敛于正态分布
最大似然估计
最大似然估计(Maximum Likelihood Estimate,MLE)
- 高斯分布最大似然估计
高斯分布的极大似然估计_Yemiekai的博客-CSDN博客_高斯分布极大似然估计

- 高斯混合分布
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。

π_k(同上方α_k)的解释(直观理解:第k个高斯所占的比重)

条件分布
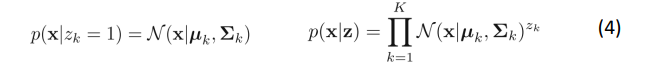
联合分布
重要!目标:不完全数据的边缘分布转换为完全数据的联合分布;其中x就是观测数据,z就是隐变量,组合到一块就是安全数据,形成的分布就叫联合分布。
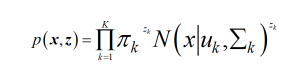
边缘分布

后验分布

GMM的对数似然函数
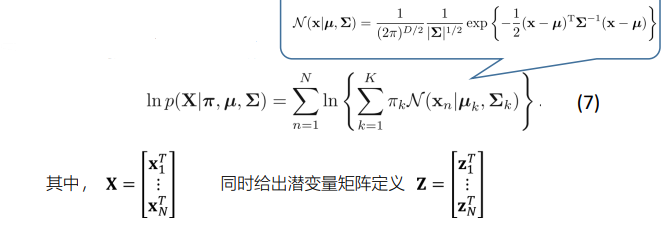
- GMM模型和K-means模型的联系

由上可知,K-means只不过是γ只能取0或者1的GMM的特殊情况。所以说,K-means是一种硬对齐方式,某个数据点只能对应到某个类别上,GMM是一种软对齐方式,使用后验概率 来表示某个数据点由某个类别产生的概率。
GMM模型参数估计的EM算法总结

四、EM模型
√ EM算法(Expectation-Maximization algorithm)初步理解

× 深入理解EM算法

疑惑?为什么这样设计Q函数?
EM算法的通用步骤

重新考虑GMM模型参数估计

EM算法的通用解释

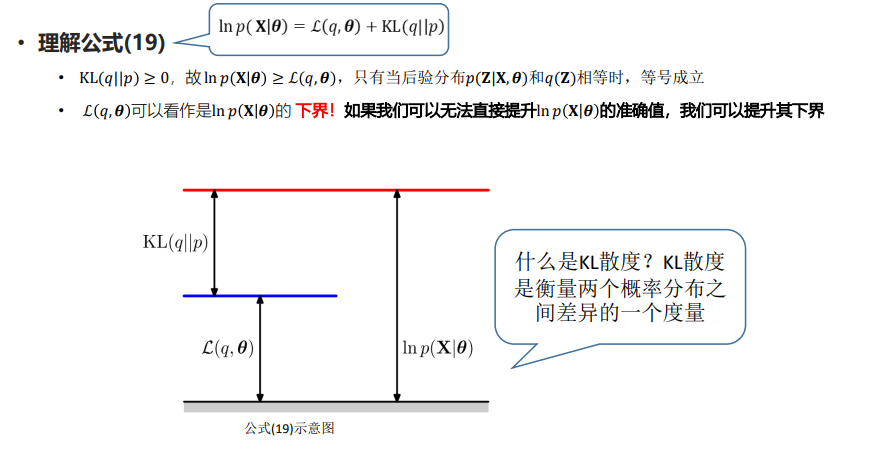
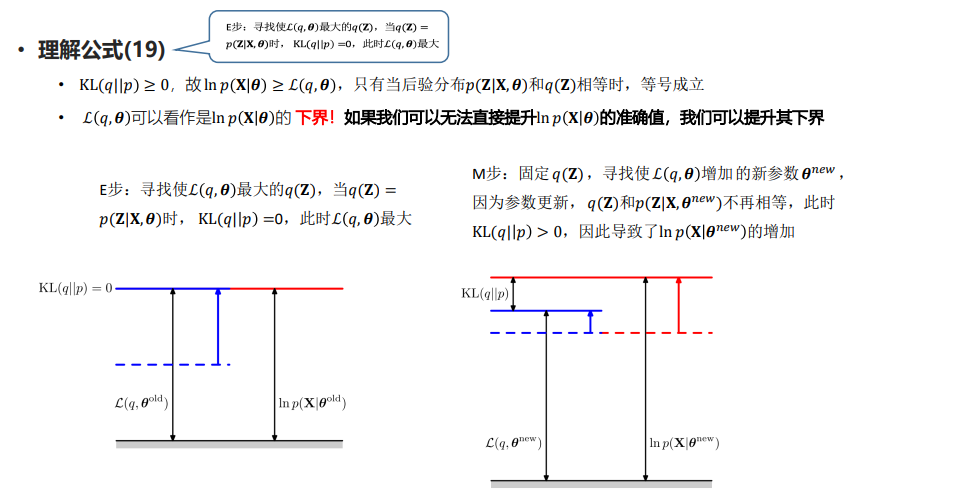
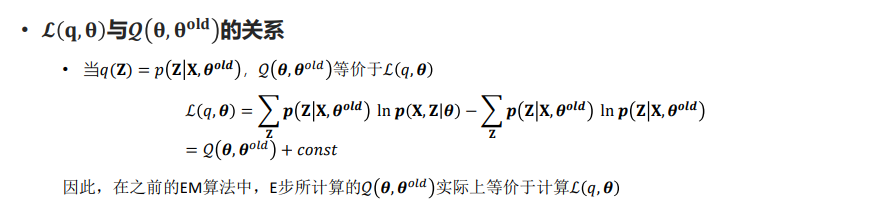
从参数空间理解EM算法
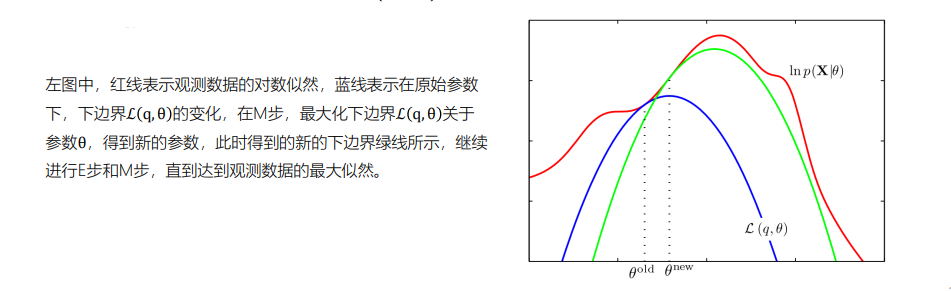
五、实践
本次作业,实现基于GMM的0(o)-9孤立词识别系统
提供的数据:本次课程提供了330句训练预料,每个英文单词(0-9,o)含有30个句子用于训练对应的GMM,所有 的训练数据和测试数据的原始音频路径、对应的抄本text(标注,0-9,o)、特征(feats.scp, feats.ark) 都在train和 test文件夹下。原始音频的39维MFCC特征已经通过kaldi提取给出,代码中也给出了读取kaldi格式特征的代码。 feats.scp 里面存储的是某句话的特征数据的真实文件和位置,特征实际存储在二进制文件feats.ark中(可以忽略 kaldi特征部分,我们已经提供了特征读取代码,读取后可在python环境中查看)
使用提供的特征,完善代码中GMM参数估计部分,并且用测试数据对其进行测试,统计错误率。每一个孤立词建立 一个GMM模型,高斯成分个数(𝐾𝐾)可以自定,特征维度是39维。