Class 2 语音信号处理及特征提取
一、数字信号处理基础
- 模拟信号到数字信号转换(ADC,analog to digital conversion)
why:生活中遇到的大多数信号都是连续的模拟信号,而计算机只能处理离散的信号,因此,必须对这些连续的模拟信号进行转化,通过采样和量化,转换成数字信号。
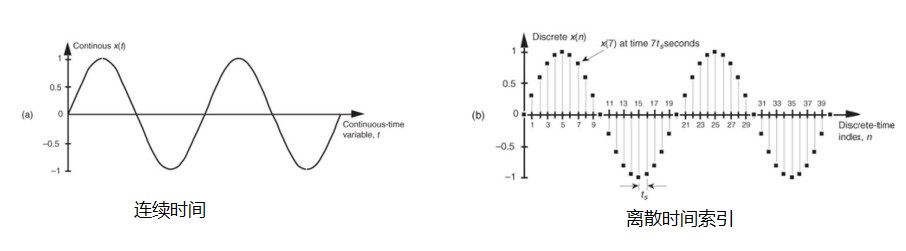
离散信号中的定义
x(t) = sin(2πf0t)
其中f0表示信号本身的频率,单位为Hz
如果我们对此正弦波进行采样,每隔ts秒进行一次采样,并使用一定范围的离散数值表示采样值,则可以得到采样后的离散信号。
x(n) = sin(2πf0nts)
其中 ts为采样周期; fs = 1/ts,为采样频率,或采样率,表示1s内采样的 点数, ts 为采样周期; n = 0,1, … … 为离散整数序列
问题:如果给定一个正弦波采样后的序列,如(b), 可以唯一的恢复出一个连续的正弦波吗?
- 频率混叠
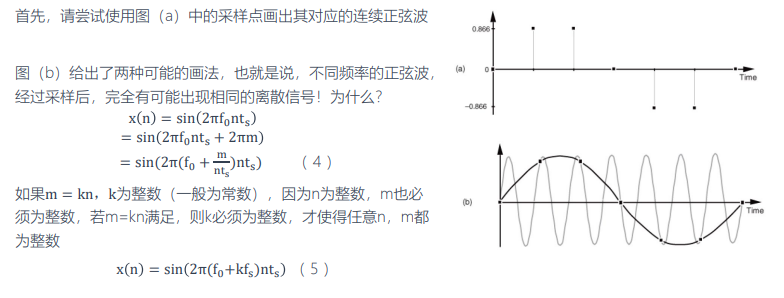
结论:如上所示原始信号频率是f0,(5)中对应的信号频率是 **f0+kfs(整数倍的信号采样频率)**,两者得到的离散序列一样。即若以同样采样周期进行采样,得到的离散序列完全一致,这种现象就叫做“频率混叠”。
- 奈奎斯特采样定律
采样频率大于信号中最大频率的两倍!fs/2 ≥ fmax
即在原始信号的一个周期内,至少要采样两个点,才能有效杜绝频率混叠问题。
- 傅里叶变换
一个非周期的信号是不存在频率的,因为频率是周期的倒数,也就是说大部分函数应该是不存在所谓的周期和频率的,然而,伟大的傅里叶证明了一个东西:任何连续的函数可以分解为很多个周期信号的线性组合。广义一点来讲就是,任意函数可表示为周期函数的线性组合,那么每个周期函数都有各自的周期,也都有各自周期的倒数(频率),傅里叶变换的工作就是把一个信号中每个周期信号通过频率展现出来。

- 傅里叶家族
只有DFT是在时域和频域上都具有离散和周期的特点, 因此,也只有DFT可以用计算机来处理。
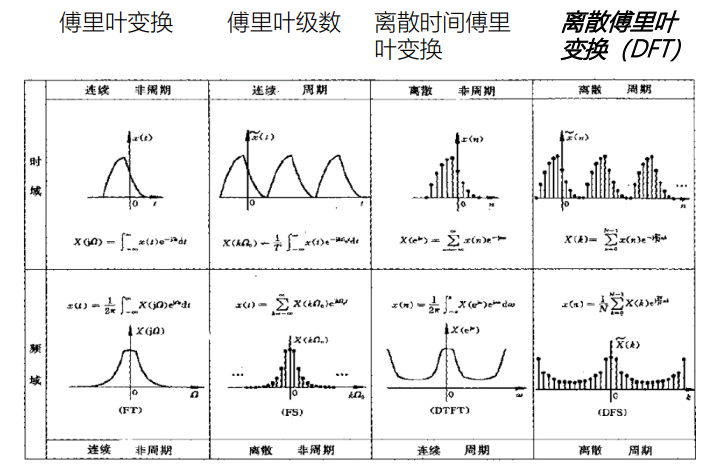
上图结论:时域上的采样(离散化),导致了频域上的周期;时域上的周期,导致了频域上的离散。
- 离散傅里叶变换

why:离散傅里叶变换(DFT,Discrete Fourier Transform)将时域信号变换到频域,在信号处理的过程中一般在频域处理更加方便,用于分析信号中频率成分。
p.s 时域离散且周期的信号才可以进行DFT;非周期离散信号需要进行周期延拓才可以进行DFT。
e.g可类比于光通过三棱镜转换为频率不同的颜色。
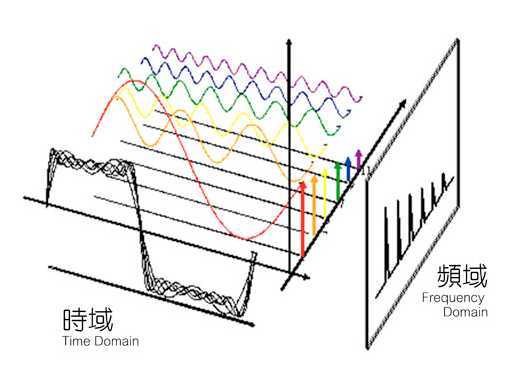
时域其实就是信号的波形随时间的变化,说通俗一点是一个自变量为时间,因变量为振幅的函数。频域也称频谱,简单来说就是自变量为频率,因变量为振幅的函数。

- DFT的性质
性质1. 对称性 X(m) = X*(N − m)
此性质很重要,如上图所示,DFT之后的离散频 率序列的幅度具有对称性,因此,在进行N点 DFT之后,只需要保留前N/2+1个点。语音信号特征提取时,一般使用512点DFT,由于对称性, 我们只需要前257个有效点。
性质2:M = A/(2/N) = AN/2
X(m)实际上表示的是“谱密度”(spectral density),即单位带 宽上有多少信号存在。如果对 一个幅度为A实正弦波进行N点DFT,则DFT之后,对应频率上的幅度 M和A之间的关系为: M = A/(2/N) = AN/2。
性质3:DFT的线性
如果x_sum(n) = x1(n) + x2(n) ,则对应的频域上有:X_sum(m) = X1 (m) + X2 (m)
性质4:时移性
对x(n)左移k个采样点,得到x_shift(n) = x(n − k),对x_shift(n)进行 DFT,有
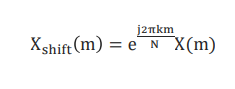
DFT的频率轴
频率分辨率:f_s/N,表示最小的频率间隔。当N越大时,频率分辨率越高。
在频域上,第m个点所表示的分析频率为:f_analysis(m) = m✖(f_s/N)。
从这个角度,我们可以理解为X(m)的幅值,体现了原信号中频率成分为m * (f_s/N)HZ的信号的强弱。
为了提高DFT频率轴的分辨率,而不会影响原始信号的频率成分。我们可以将时域长度为N的信号 x(n) 补0,增加信号的长度,从而提高频率轴分辨率。对信号进行补0的操作,不会影响DFT的结果, 这在FFT(快速傅里叶变换)中和语音信号分析中非常常见。
- 快速傅里叶变换(FFT)
FFT的基本思想是把原始的N点序列,依次分解成一系列的短序列。充分利用DFT 计算式中指数因子 所具有的对称性质和周期性质,进而求出这些短序列相应的 DFT并进行适当组合,达到删除重复计算,减少乘法运算和简化结构的目的。
二、特征提取流程

Fbank和MFCC(Mel-Frequency Cepstral Coefficients)特征目前仍是主要使用的特征,虽然有工作尝试直接使用波形建模,但是效果并没有超越基于频域的特征。
Step1 预加重(pre-emphasis)
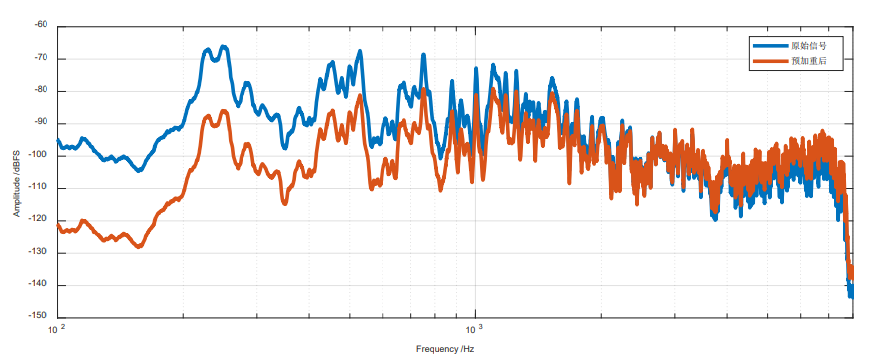
why:提高信号高频部分的能量,高频信号在传递过程中,衰减较快,但是高频部分又蕴含很多对语音识别有利的特征,因此,在特征提取部分,需要提高高频部分能量。
预加重滤波器实质上是一个一阶高通滤波器,低频 信号(即时域上信号变换慢的信号)将被抑制。给定时域输入信号𝑥[𝑛],预加重之后的信号为 𝑦[𝑛] = 𝑥 [𝑛]− 𝛼x[𝑛 − 1],其中,0.9 ≤ 𝛼 ≤ 1.0
Step2 加窗(windowing)分帧
why:语音信号为非平稳信号,其统计属性是随着时间变化的;语音信号又具有短时平稳的属性,在一个发音单元里,语音信号表现出明显的稳定性,规律性;在进行语音识别的时候,对于一句话,识别的过程也是以较小的发音单元 (音素、字、字节)为单位进行识别,因此用滑动窗来提取短时片段。
分帧的过程,在时域上,即用一个窗函数和原始信号进行相乘 y[n] = w[n]x[n]
w[n] 称为窗函数,常用的窗函数有 矩形窗, 汉明窗 (Hamming)
加窗主要是为了使时域信号似乎更好地满足 FFT 处理的周期性要求,减少泄漏。
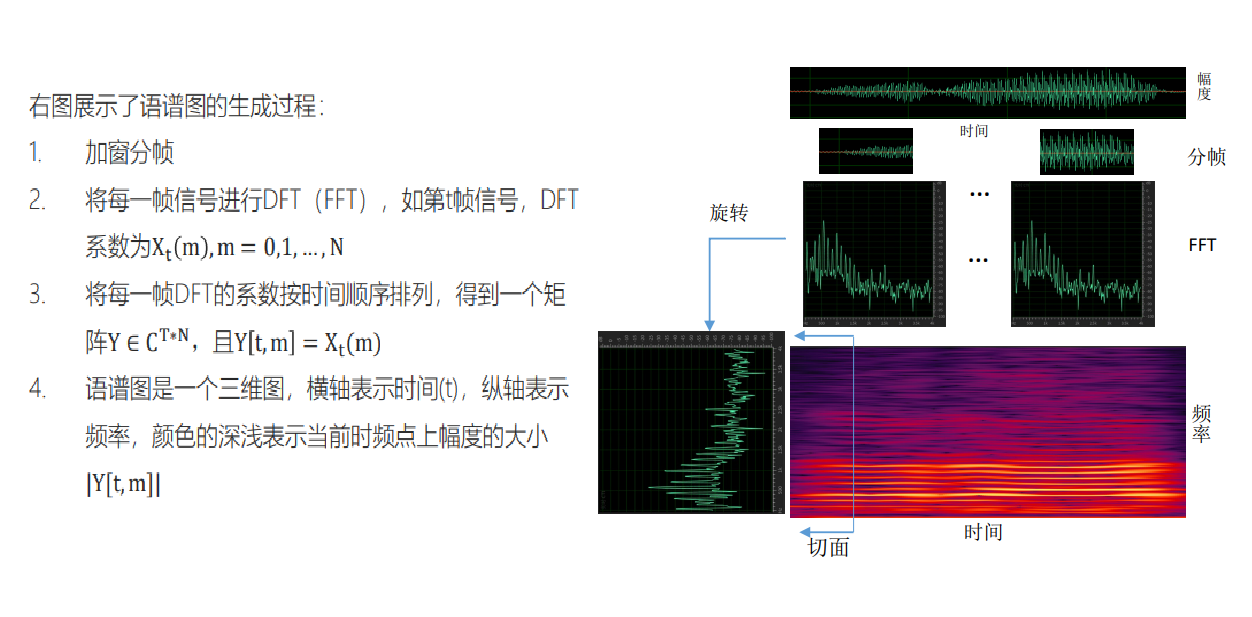
Step3 傅里叶变换
将上一步分帧之后的语音帧,由时域变换到 频域,取DFT系数的模,得到谱特征。
Step4 梅尔滤波器组和对数操作
- DFT得到了每个频带上信号的能量,但是人耳对频率的感知不是等间隔的,近似于对数函数
- 将线性频率转换为梅尔频率,梅尔频率和线性频率转换关系

- 梅尔三角滤波器组:根据起始频率、中间频率和截止频率,确定各滤波器系数
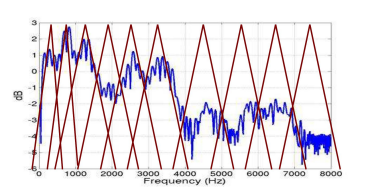
梅尔滤波器组设计
- 确定滤波器组个数P
- 根据采样率fs,DFT点数N,滤波器个数P,在梅尔域上等间隔的产生每个滤波器的起始频率、中间频率和截至频率,注意,上一个滤波器的中间频率为下一个滤波器的起始频率(存在overlap)
- 将梅尔域上每个三角滤波器的起始、中间和截止频率转换线性频率域,并对DFT之后的谱特征 进行滤波,得到P个滤波器组能量,进行log 操作,得到Fbank特征
MFCC特征在Fbank特征基础上继续进行IDFT变换等操作
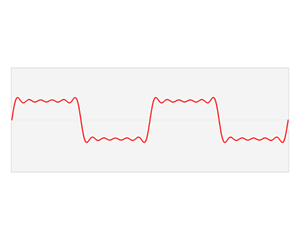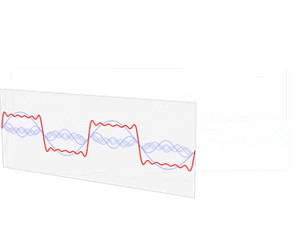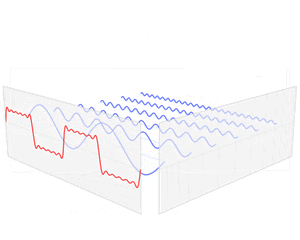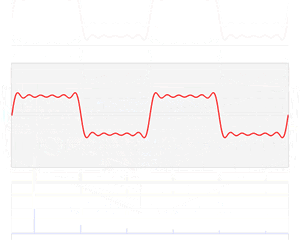
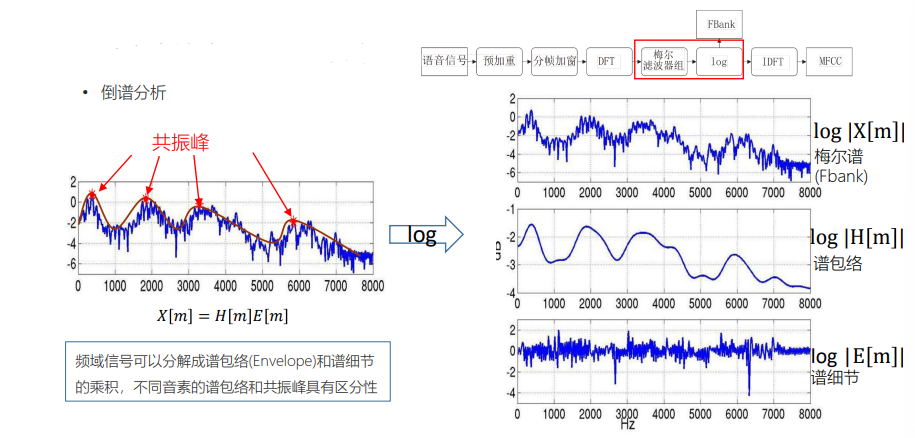
- 倒谱分析
FBank 特征的频谱图大概长下面这个样子,图中四个红点表示的是共振峰,是频谱图的主要频率,在语音识别中,根据共振峰来区分不同的音素(phone),所以我们可以把图中红线表示的特征提取出来就行,移除蓝色的影响部分。其中红色平滑曲线将各个共振峰连接起来,这条红线,称为谱包络(Spectral Envelope),蓝色上下震荡比较多的线条称为谱细节(Spectral details)。
频域信号可以分解成谱包络(Envelope)和谱细节的乘积,不同音素的谱包络和共振峰具有区分性。
- IDFT,逆傅里叶变换
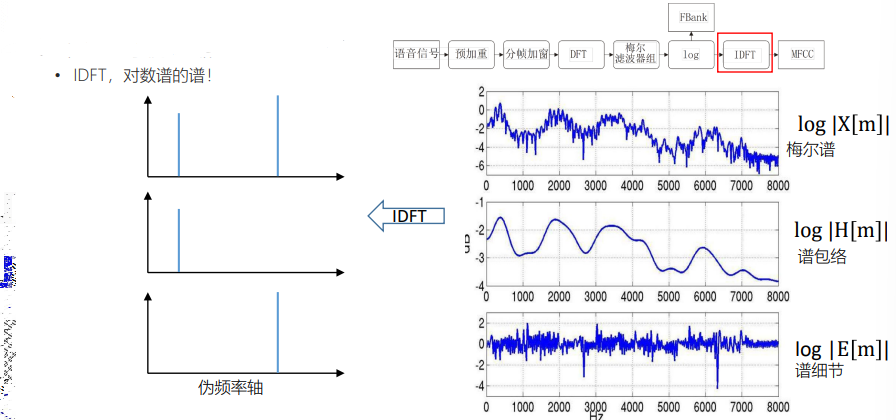
- |𝑋[𝑚]| = |𝐻[𝑚]| |𝐸M|
- log |𝑋[m]| = log |𝐻[𝑚]| + log |𝐸[𝑚]|
- 两边进行IDFT
- IDFT之后的第1~K个点,为 K 维MFCC特征
取log有两个目的:
- 人耳对信号感知是近似对数的
- 对数使特征对输入信号的扰动不敏感
Step5 动态特征计算
- 一阶差分(Delta, Δ),类比速度,最简单的一阶差分计算方法
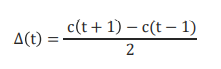
- 二阶差分(Delta delta, ΔΔ),类比加速度,简单计算方法
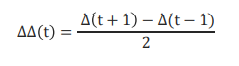
Step6 能量计算
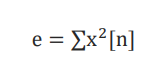
三、总结

一帧信号,通常为20 ~ 50 ms
微观上足够长:至少包含2~3个周期
宏观上足够短:在一个音素之内
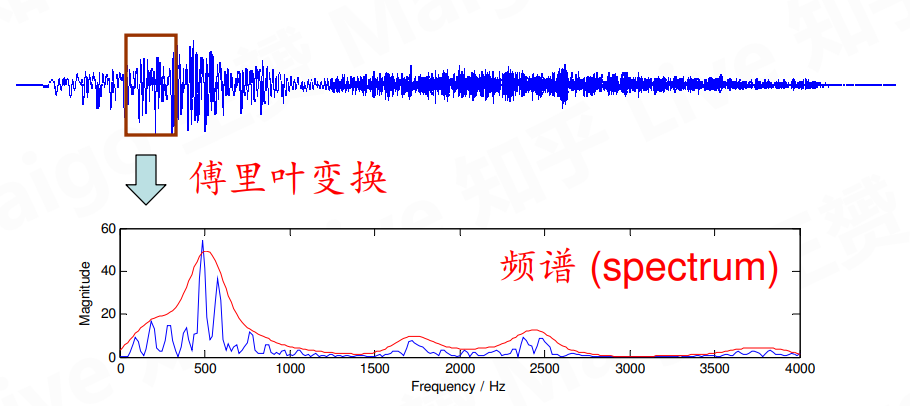
频谱具有精细结构和包络
精细结构反映音高,用处较小(次要)
包络反映音色,是主要信息
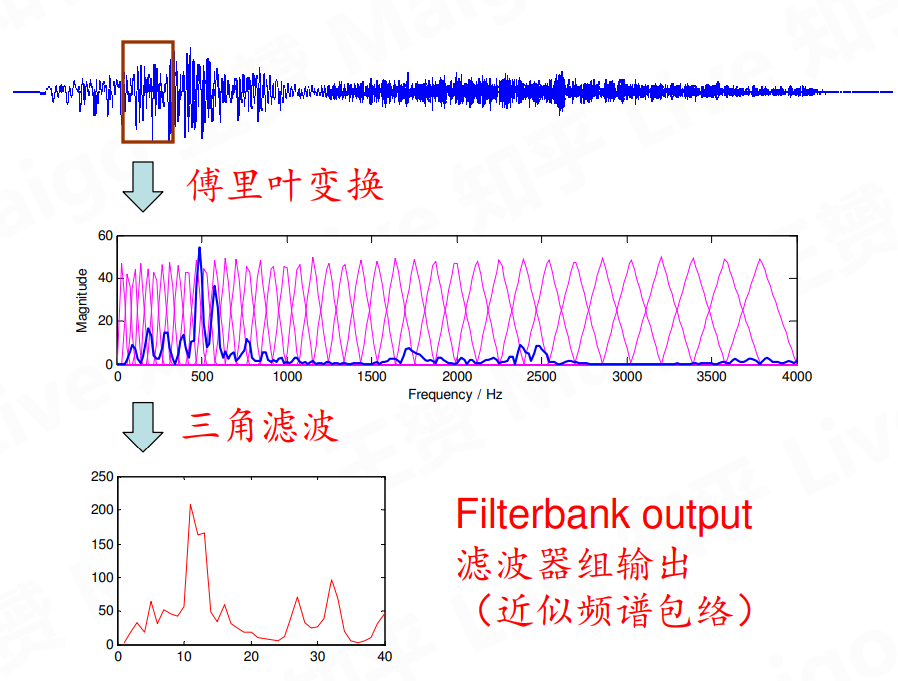
三角滤波的结果Fbank
将精细结构做了平均
计算每个三角形内部总幅度(能量)
三角形左密右疏
人耳👂的频率特性,人耳对低频信号敏感,分辨率比较高
高频则分辨率较低,三角形比较细
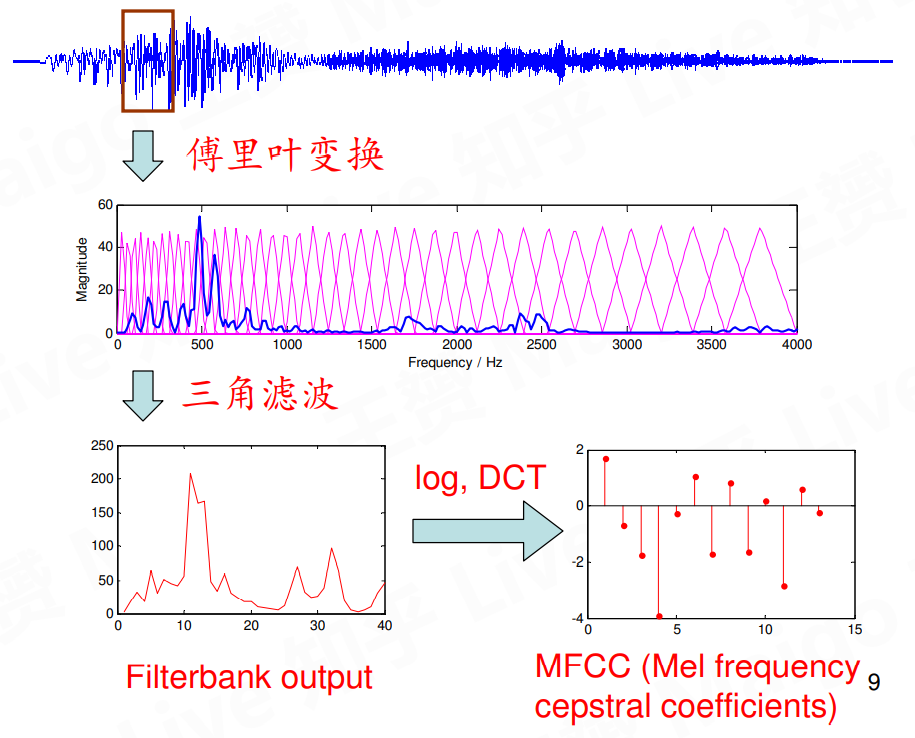
得到MFCC
Fbank基本可以作为语音识别的特征,进一步进行数学变换,即取对数和离散余弦变换,将filterbank压缩成更小规模,得到13维向量的MFCC
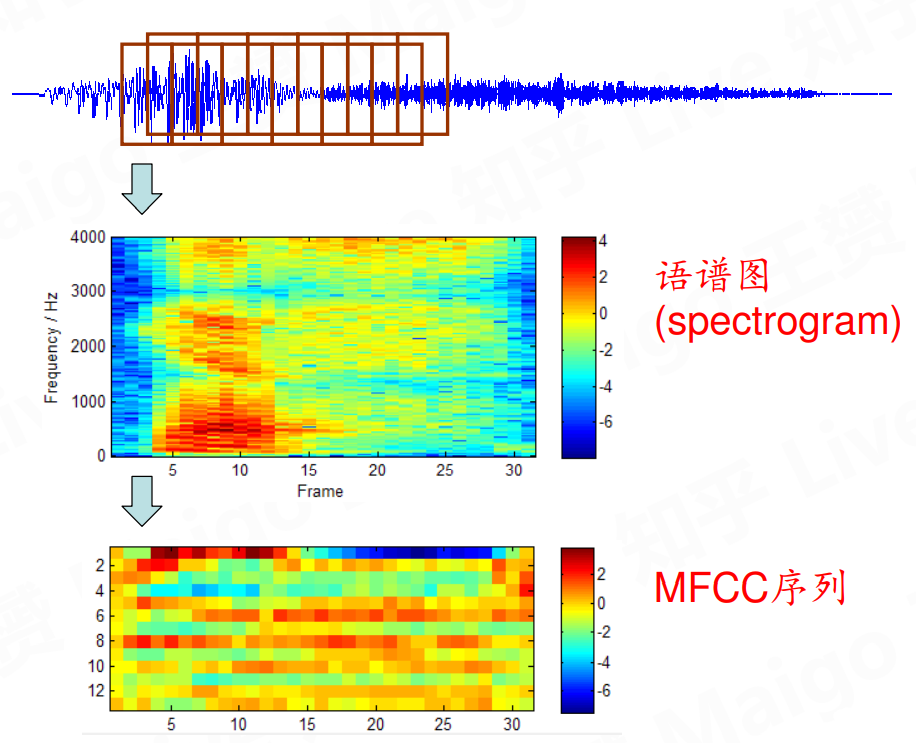
MFCC序列是最常用的特征
主要描述频谱包络
优点:排除基频,符合听觉,维度低
缺点:视野小,受噪声、回声、滤波影响严重
改进:加入一阶(视野小,上下文)、二阶差分;各种归一化(回声滤波)
四、实践作业
Q1: 如果对语音模拟信号进行采样率为16khz对采样,得到的离散信号中包含的最大频率是多少?
A:8khz
Q2: 对一个采样率为16k的离散信号进行下采样,下采样到8k,为什么要先进行低通滤波?
A:因为根据奈奎斯特采样定律,采样率为16k的离散信号中可能存在频率不超过8k的信号;下采样到8k,音频中只允许存在最大频率不超过4khz的信号,所以需要首先进行低通滤波过滤掉其中超过4khz的高频信号。
Q3: 时域上的采样(离散化),导致了频域上的周期,为什么?
A:频域的周期性本质是高低频之间频谱混叠的一种表现。在时域上确定一组采样点后,可以通过提高频率使无穷多组信号波通过这些采样点,通过傅里叶变换不同区分这些不同频率的信号,这在频率上就体现为高频信号和低频信号的幅值相同,从而表现出周期性。
Q4: 时域上的周期,导致了频域上的离散,为什么?
A:频域的离散本质是只有有限个频率有信号输出。时域上周期性的信号可以由有限个正弦波组成,由傅里叶变换的性质可知,信号在频域上频率值和幅值是这些正弦波的频率和幅值分别决定,有限个正弦波映射到频域上,表现为频率信号为离散的。
Q5: 编程题:给定一段音频,请提取12维MFCC特征,阅读代码预加重、分帧、加窗部分,完善作业代码中 fbank和mfcc部分,并给出最终的Fbank和MFCC特征,用默认的配置参数,无需进行修改。