基于LSTM神经网络的股票价格趋势预测的研究与实现
摘要
股价走势预测一直是金融领域的热点问题,受到学术界和工业界的广泛关注。 由于股票价格的非平稳性和高波动性,这是一项具有挑战性的任务。传统的股票价格预测方法基于统计分析模型和机器学习模型。近年来,深度学习方法的快速发展及其在图像分类、语音识别和自然语言处理(NLP)等各个领域的成功应用。Jeffrey L. Elman提出了循环神经网络(RNN)来处理序列数据;但是,它会导致梯度消失问题。为了缓解这个问题,Jurgen Schmidhuber提出了作为 RNN 的一种变体的长短期记忆(LSTM)网络,LSTM是一种增加循环神经网络记忆的模型,循环神经网络具有短期记忆,通过使用门控机制来学习长期依赖关系。
预测股票价格趋势的传统方法大多基于历史 OHLC(即开盘价、最高价、最低价和收盘价)数据。但是,它消除了大部分交易信息。为了解决这个问题,在本文中,基于历史 OHLC数据,我们又增加了VM(即交易量和交易金额)。在本文中,基于LSTM 的模型被应用于研究 OHLCVM 与股价之间的关系并预测股价趋势。主要是考虑使用时间序列数据,应用LSTM模型从一系列历史数据中提取特征。然后,我们通过数据预处理使其信息保留丰富的特征,以更好地表示股票价格的变化。最后,应用整个模型,并通过不断优化调参以及超参数优化操作,针对每只股票找到最优参数,利用记忆时长的数据特征来预测股价走势。
通过使用中国股票市场的真实股价数据,实验结果验证了LSTM模型对股票预测的有效性。
关键词:神经网络;LSTM;股票价格;趋势预测;参数优化
一、绪论
1.1研究背景和意义
股票投资者打算探索和总结潜在的交易模式以预测股票价格趋势以最大化获得的利润。因此,准确预测金融领域的价格走势成为热门话题。然而,由于股票市场是非平稳的,容易受到各种不确定因素的影响,预测股票价格具有挑战性和难度[1]。随着金融机构开始接受人工智能,机器学习越来越多地用于帮助做出交易决策,越来越多的金融经济学家甚至数据算法分析师开始关注研究各种历史数据,包括宏观经济数据信息、股票交易价格等,以期从中发现规律。通过建立定量和预测模型来分析股价走势。关于股票价格预测,现有的大部分工作都是基于股票的历史 OHLC(即开盘价、最高价、最低价和收盘价)数据。 OHLC数据虽然在一定程度上保留了市场走势的趋势特征,但剔除了大部分详细的交易信息。
尽管有大量股票数据可供机器学习模型训练,但高信噪比和众多影响股票价格的因素是预测市场困难的几个原因。同时,这些模型不需要达到很高的准确度,因为即使是 60% 的准确度也可以带来可观的回报。但是基于布朗运动,股票价格的未来变化与过去无关。因此,不可能预测确切的股票价格,但可以预测和捕捉向上和向下的趋势。
1.2国内外研究现状
目前,金融市场是一个嘈杂的、非参数的动态系统,股票价格的预测方法主要有两种:传统的分析方法和机器学习方法[2]。传统的计量经济学方法或带参数的方程不适用于分析复杂、高维和嘈杂的金融序列数据。
近年来,神经网络在股票预测中已成为一个热点问题,因为它可以在不依赖先验知识的情况下,从大量高频原始数据中提取数据特征。1988年,White 利用神经网络对 IBM股票进行了预测,但试验结果却不理想[3]。2003年,Peter Zhang分别使用神经网络和自回归综合移动平均模型(ARIMA)预测股票。实验结果表明,神经网络在非线性数据预测方面具有明显优势,但准确度仍有待提高[4]。2005年,梁艳春等人提出了一种基于神经网络的时间序列预测方法。该方法结合了最优分区算法 (OPA) 和径向基函数 (RBF) 神经网络[5]。2014 年,Adhikari 等人提出了一种结合随机游走(RW)和人工神经网络(ANN)的方法来预测四个金融时间序列数据,结果表明预测精度有一定的提高[6]。2018年,张黎等人提出了基于LM-BP神经网络的股票价格预测网络结构,改善了传统BP神经网络训练算法训练速度慢、精度低的缺点[7]。2018年,黄宏运等人的实验结果表明卷积神经网络可以预测时间序列,深度学习更适合解决时间序列问题。然而,由于 CNN 更常用于解决图像识别和特征提取,因此单独使用 CNN 的预测准确率相对较低[8]。2020年,Kamalov 使用 MLP、CNN 和 LSTM 预测了美国四大上市公司的股价。实验结果表明,与预测价格变化方向的类似研究相比,这三种方法显示出更好的结果[9]。2020年,薛艳等人建立了基于LSTM深度神经网络的金融市场时间序列高精度短期预测模型,并与BP神经网络、传统RNN和改进的LSTM深度神经网络进行了对比[10]。
基于以上结果表明,LSTM 深度神经网络具有较高的预测效果和精度,对于有效地预测股市的时间序列具有较好的时效性和泛化性。
1.3研究内容和方法
本文基于当前流行的深度学习理论,研究了在TensorFlow中的Keras深度学习框架下基于LSTM深度神经网络的股票价格时间序列的模型构造与预测,详细介绍LSTM模型的原理、TensorFlow的特别结构以及影响训练模型结构的重要参数因素,最终构建基于LSTM神经网络模型的股票价格趋势预测模型。模型网络结构方面,调节学习率、批数据量、神经元数量、神经网络层数以及训练选代次数等参数,对基本训练出来的结果与优化后的模型进行对比分析,并通过超参数优化选择最合适的超参数,不断提升模型预测精度,通过回调函数记录最优模型并做出股票价格预测可视化。
二、相关理论
2.1影响股价因素及预测难点
近年来,机器学习和深度学习已成为金融数据分析的流行方法,包括金融文本数据、数值数据和图形数据。金融领域最流行和最复杂的深度学习之一是未来股票预测。造成未来股票预测的难点在于,同时影响股票涨跌幅度和频率的不同因素太多[11]。股票价格数据具有时间序列特征,股票价格的变化趋势长期作为经济领域重量级别问题,确定影响股票价格波动的原因,有利于更好地调整输入特征,从而有利于更好地预测股票价格趋势。通常股票价格受以下几种因素影响:
(1)经济因素
除利率、汇率、通货膨胀率、交易量、年回报率等上市公司基本面数据外,历史数据和成交量、价格趋势分析,也是预测金融股的预测因素上市公司、国家股指和地区股指的市场价格和交易量。
(2)政治因素
很多国家的重大事件政治局势或国际事务也可能影响股价。例如,在乌克兰局势动荡加剧后,欧洲亚洲甚至全球股市就受到波动,股市蒸发约1亿美元。
(3)公司自营业绩
另外,公司本身科技产能销量的提升会很大程度上吸引外来投资,从而导致市场波动,直接引起股价上涨。例如,当苹果发布一款新产品时,很多人都想购买它,通常它的性能很快就会好起来。因此,更多的人对苹果股票感兴趣,然后,苹果股票需求增加,这将导致苹果股价上涨。
(4)行业市场因素
全球产业的变动会对经济和股价的变动产生影响。例如,能源开采存储任何一环节的成本上升都会导致销售额整体收益下降、行业整体利润下降和该能源全球行业股价受到波动而导致的下跌。此外,恐怖行动还会造成经济活动的停滞,甚至会造成股票价格的下降。
(5)投资者个人心理因素
投资者的情绪和信心可能引起股市的上升和下降,进而造成股票价格的上升和下降[12]。股票市场的总体趋势会对股价产生影响:
- 牛市–股票价格上升,投资者信心增加。这往往与经济复苏、经济繁荣和投资者的乐观联系在一起。
- 熊市–股票市场处于松弛状态,价格正在下跌,投资者的信心正在消退。这种情况经常发生在经济衰退、失业率高、物价上涨时期。
然而,影响股票供需的主要因素有几个,如公司新闻、公司业绩、行业表现以及投资者情绪。如果我们关注主要因素,追溯历史股价,我们或许可以相当准确地预测未来的股价[13]。人们通常对股票因素的记忆很短。因此,确定合适的历史窗口大小对于正确预测股票价格很重要。如果窗口大小与人类记忆相比太大,许多因素或新闻被投资者遗忘,已经过时,预测不会好。另一方面,如果窗口与人的记忆相比太短,很多窗口外的消息或情绪仍留在人们的大脑中,预测也会很糟糕。因此,错误的历史窗口大小不利于我们成功的股价预测。
2.2深度学习
2.2.1长短期记忆神经网络
神经网络是一套类似于人脑的运算法则,用来辨识模式。他们通过机器感知、标记或对原始的输入进行聚类。他们能够辨认出矢量中所包含的所有数据(图像,声音,文字,时间),都必须转化为它们。人工神经网络由大量高度互连的处理元素(神经元)组成,它们协同工作以解决问题,人工神经元结构如下图2-1所示。

循环神经网络是具有内部记忆的前馈神经网络的泛化。RNN 本质上是循环的,因为它对数据的每个输入执行相同的功能,而当前输入的输出取决于过去的计算。生成输出后,将其复制并发送回循环网络。为了作出决定,它会考虑当前输入和它从先前输入中学到的输出。与前馈神经网络不同,RNN 可以使用其内部状态(内存)来处理输入序列。 这使得它们适用于诸如未分段、连接的手写识别或语音识别等任务。在其他神经网络中,所有输入都是相互独立的。但是在 RNN 中,所有的输入都是相互关联的[14]。
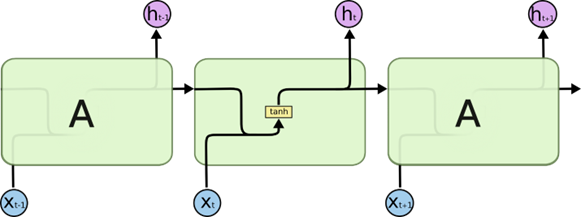
但是循环神经网络存在梯度消失和爆炸以及不能处理很长序列的问题,长短期记忆 (LSTM) 网络是是一种特殊的 RNN类型,能够学习长期依赖记忆关系,LSTM结构如上图2-2所示。LSTM 被明确设计为避免长期依赖和梯度爆炸问题,RNN的梯度消失问题也在这里得到了解决。LSTM 非常适合在给定未知持续时间的时间滞后的情况下对时间序列进行分类、处理和预测,它通过使用反向传播来训练模型[15]。在 LSTM 网络中,存在三个门:
- 遗忘门层:发现要从块中丢弃的细节,遗忘门层结构如下图2-3所示。
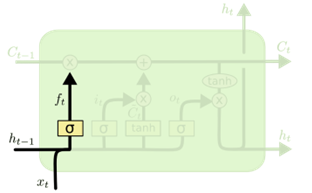
- 输入门层:发现应该使用输入中的哪个值来修改内存,输入门层结构如下图2-4所示。

- 输出门层:块的输入和内存用于决定输出,输出门层结构及计算如下图2-5所示。

于是综上所述:所有的参数就是在于四个w和 b,其中 ![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
2.2.2激活函数Relu
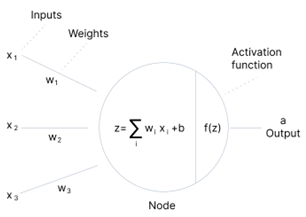
在神经网络和深度学习中,激活函数在激活隐藏节点以产生更理想的最优化模型输出发挥着重要作用,神经网络计算结构如下图2-6所示。激活函数引入将非线性特性模型的主要目的是使模型不仅局限于线性规划而引入更多可能,激活函数负责激活函数的主要作用是将来自节点的加权总和输入转换为输出值,以馈送到下一个隐藏层或作为输出。
Sigmoid 和 tanh 是单调的、可微分的,并且是以前更流行的激活函数。然而,这些函数会随着时间的推移而饱和,这意味着对于 tanh 和 sigmoid,较大的值会捕捉到 1.0,而较小的值会捕捉到 -1 或 0。此外,这些函数仅对其输入中点附近的变化真正敏感,这会导致梯度消失的问题。克服这个问题的替代和最流行的激活函数是整流线性单元 (ReLU)。
ReLU (整流线性激活函数)是一个分段线性函数,如果输入为正则直接输出,否则输出零。ReLU函数方法的出现简化了计算的复杂性,对加速网络计算具有巨大的作用。
其数学表达式为:f(x)=max(0,x)
通过ReLU函数可以将一个值域在 区间的数组映射到了 区间,ReLu函数图像如下图2-7所示。并且ReLU 的计算成本低于 tanh 和 sigmoid,因为它涉及更简单的数学运算。由于使用该模型,可以更易于训练和提高性能,所以已经成为很多类型的神经网络的缺省激活功能[16]。
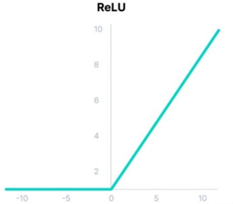
2.2.3模型参数
在神经网络的训练中,参数是我们学习的最终目标,而最基础的是神经网络的权重w和偏移量b,而深度学习则是为了寻找一组更好的参数,以达到对未知结果的预测,我们不需要人工调整这些参数,而是在训练的时候自动更新生成的,是由前面提到的优化器来实现的。
超参数是我们用来控制模型结构、功能、效率等的调节器。网络模型优化调整的目标是寻求全局最优(或与之比较),而规则项则要求模型尽可能地接近最优。一般来讲,这两种方法都有一些矛盾,但是它们的目的都是使预期危险降到最低。在模型优化中,最大限度地减少了经验风险,同时也存在着过度拟合的问题。因此如何使二者的关系达到最佳或更好的结果就成为了超参数调整的目标。在机器学习环境中,超参数值是在学习过程开始前设定的一个参数,而非由训练所得的参数。一般情况下,为了改善学习效果,必须对超参量进行优化,为学习机选取一套最佳的超参量。深度学习中的超参量,如学习率(Learning Rate)、批大小(Batch Size)、神经网络深度(Layer)等[17]。
这其中最大的区别就在于,要不要用数据来调节,一般都是用数据来控制,而不是用数据来控制,而是用来调节的。比如,卷积核心的特定的核心参数,是由数据驱动的。而学习速度,就是一个人工调节的超级参数。比如,卷积核心的特定的核心参数是由数据驱动的;而学习率是一个人工调节的超参数。
在设定超参数时,可以采用人工、网格、随机等方式。网格搜寻就是当有三个以上的超参数值时,最常用的就是栅格搜寻。用户可以为每一个超参数值选取一组更小的有限值来进行研究。然后利用超参量的笛卡尔卡尔乘积,生成一套超参量的超参量集合,进行网格搜索。选取具有最小错误的校验集合为最佳超参量。随机查找就是当超参数太多时,我们先定义一个边界分布,然后对其进行搜索。无论是网格还是随机搜索,都没有充分利用各种超参数的关联。
2.3Tensorflow深度学习框架
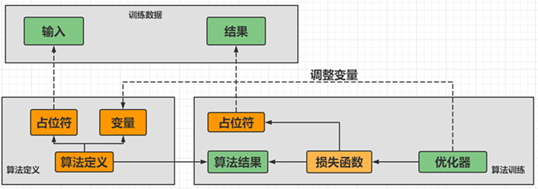
TensorFlow能够训练和执行手写数字分类,图像识别,单词嵌入,循环神经网络,序列到序列模型,自然语言处理,以及基于偏微分方程(PDE)的仿真。除此之外, TensorFlow还可以通过同样的模式来进行大量的生产预测。TensorFlow一般完成一个深度学习模型的设计需要以下四个步骤:第一步是准备输入数据并做好数据集的划分,第二步是定义深度学习模型的结构,第三步是使用优化器、损失函数和评价函数训练模型,第四步是模型的优化评估与应用。
TensorFlow 是一个开源的端到端平台,一个用于多种机器学习任务的库,其优势在于能在多个CPU或GPU,或者两者混合运行。得益于其完善的框架和大量训练有素的模型和教程,TensorFlow 是许多行业专业人士和研究人员最喜欢的工具,TensorFlow流程图如下图2-8所示。TensorFlow 的一个重要特性是 TensorBoard,TensorBoard 能够以图形和视觉方式监控,让开发人员能够更好地调试并跟踪训练过程,因此受到了学术界和产业界的高度关注。
Keras是一种基于 TensorFlow的先进的神经网络类库,它为建模和培训提供了先进的 API,而且 Keras更易于使用。本论文的重点在于利用 TensorFlow中的 Keras深度学习框架来构造 LSTM的深度网络模型,与传统平台相比,极大地提高了学习效率[18]。
三、基于LSTM的股价预测模型设计与实现
3.1数据选择与预处理
3.1.1数据选取
数据的下载使用的是 JoinQuant 平台,JQData是专门为金融机构、学术研究、定量交易者、聚宽数据团队所设计的金融数据服务的界面。通过 JQData,可以快速、便捷地查询、计算财务数据,满足各类财务数据的需要。在数据方面,根据客户的需要,JQData提供沪、深圳市场、上市公司、场内资金、场外资金、股指、期货、期权等综合金融信息;在数据格式上,不同品种同一属性的数据用同一个接口就能获取,简化了代码,从而减少了用户学习成本,大大提高用户工作效率[19]。
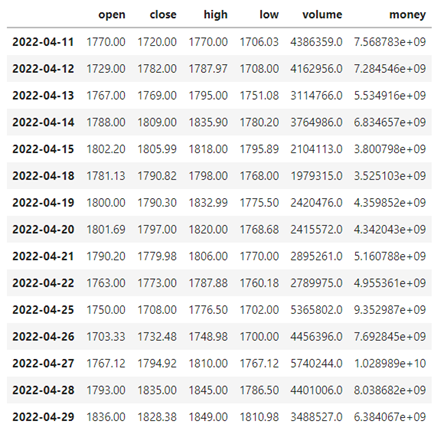
本文选取贵州茅台(600519.XSHG)、万科A (000002.XSHE)、云南白药(000538.XSHE)以及紫光国微(002049.XSHE)四只股票,在聚宽平台获取其从2006年5月1日到2022年5月1日的股票数据,包括日期(Date)、开盘价(Open)、收盘价(Close)、最高价(High)、最低价(Low)、交易量(Volume)以及交易金额(Money)。茅台从2020年4月11日到2022年4月29日交易日的股票数据信息如下图3-1所示。
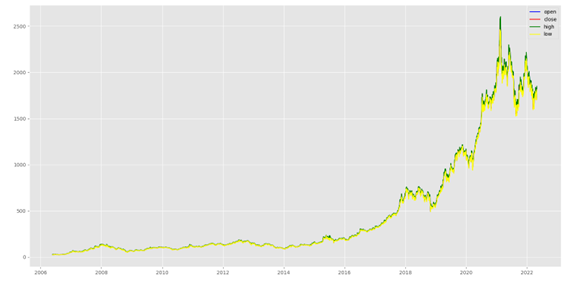
在选取的四只股票中,贵州茅台(600519.XSHG)一直处于A股第一高价股,并且通过研究学习发现,随着贵州茅台在技术上的不断创新以及营销手段上的不断改革,在2022年至2030年期间,其股价仍能保持良好增长,并一直处于高端白酒龙头地位。由于其独特的工艺和稀缺性导致其具有一定收藏价值,也将会源源不断地受到投资者的青睐。下图是使用matplotlib库绘制的2006—2022年贵州茅台股票开盘价(Open)、收盘价(Close)、最高价(High)以及最低价(Low)的价格走势图,其中横轴是时间,纵轴是价格,由下图3-2所示中价格趋势线的走势情况我们也可以初步判定茅台在未来几年仍会保持不断上涨状态[19]。
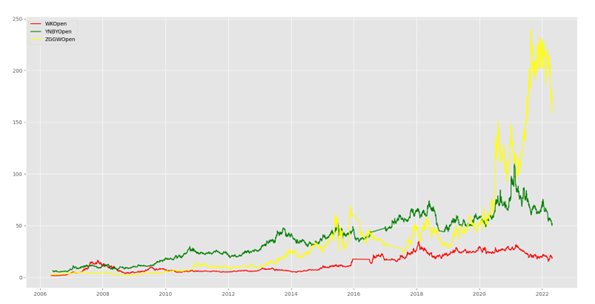
正如下图3-3其他三只股票的交易日收盘价走势所示,同一段时间内,尽管相比贵州茅台因价格悬殊所以股票价格变化趋势相差较大,万科A (000002.XSHE)、云南白药(000538.XSHE)以及紫光国微(002049.XSHE)三只股票中,云南白药和紫光国微股票价格处于上涨趋势,万科股价处于低迷状态。由于疫情因素,在防护用品需求激增、供需矛盾异常突出的情况下,云南白药作为药企不断紧急调集物资,组织原料,克服重重困难恢复生产,全力支持一线,获得社会一致关注和称赞,其股价也在疫情期间一直处于上涨水平[21];由于政治因素,美国等西方国家加大对我国高端技术领域制裁打压,我国近两年芯片领域整体股价一直也处于上涨状态,作为国内领先的智能芯片公司,多家券商对此给予了一致的评价[22];自2016年中央经济工作会议首提房住不炒,并在2018年写入政府工作报告后,“房住不炒”连续四年出现在政府工作报告中,万科作为房地产企业,股价势必因此受到冲击,但因房地产其本质还是一种“不变资产”,其股市仍处于一种稳定状态[23]。
3.1.2 数据预处理
由于聚宽平台提供的数据已基本有序且整洁,因此数据预处理只需要简单地对数据进行一下处理即可。由于对数据进行标准化之前需要将空值进行处理,所以首先使用pandas库读取之前下载的四只股票的历史数据信息,分别对其读入的DataFrame进行信息查看,调用info函数查看数据缺失以及数据类型情况,然后,利用 dropna函数将数据块中的空白值进行初始整理。
本次深度学习预测的目标是是对未来几个交易日的预测,在股票数据信息中相比于开盘价和最高最低价,收盘价更具代表性,因此我们选用收盘价作为新的一列预测值,并初步将预测偏移时长pre_days设为10个交易日。
接着进行标准化处理,数据标准化是为了消除特征间单位和尺度的影响,这有助于提高我们模型的性能,加快了加权参数的收敛性。以消除各特点的差别,本文使用 Scikit-Learn 的 Standardization标准化,将特征数据的分布调整成标准正态分布。当然其实质就是指标准差标准化,即(x-x.mean())/x.std(),std在一定程度上代表了数据的“跨度”,可以理解为取值范围,也可以理解为量纲,除以标准差就是消除量纲。
3.1.3构造数据特征向量
输入特征数据应该以3D数组的形式输入到 LSTM 模型中,首先设置一个记忆天数memory_days为 30,即以30个时间步创建数据。在这里我们引入数据结构中的固定长度队列概念,即滑动窗口机制,以30个交易日数据为一组输入数据,它的实质是一个固定尺寸的队列,在添加了新的元素后,该队列中最旧的元素会被自动删除。这样依次遍历所有数据,例如在贵州茅台数据中,原数据共计3864条,依次遍历完共构建3825条输入特征。这样我们就把数据转换为一个(3825,30,6)的 3D 数组的输入特征向量,其中包含 X_train X_test样本、30 个时间戳的每一步的一个特征和对应目标值为一个(3825,)的target输出特征向量。
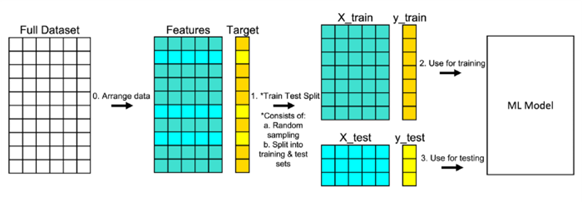
如果要判断一个模型的好坏,最好的方式就是通过泛化误差进行判断,期望所选择模型的泛化误差越少越好。然而,在工程实践中,一般不能直接求出广义误差,而且由于存在着过拟合问题,无法用来判定广义误差,因此需要一个全新的样本来进行测试。在本次深度学习预测模型中,将原数据拆分为训练集和测试集,而测试机就作为这个全新的样本,尽管数据集划分有很多方法,如留出法交叉验证法、自助法等。但由于本次实验股票数据量较大,选择的是留出法将数据按照4/5样本划分,使用的是Scikit-Learn 的model_selection包的train_test_split函数,其中训练数据集用于拟合机器学习模型,测试数据集用于评估拟合机器学习模型,数据集的划分流程如下图3-4所示。
3.2模型设计
本文使用TensorFlow中 Keras 的Sequential 建立有三层隐藏层的LSTM模型,为防止过度拟合在每一层的后面添加了DropOut层。其中输入层采用LSTM输入,将预处理好的3D数组数据特征输入,第一层为80个神经元的LSTM层,每个lstm单元都输出hidden layer,第二层为100个神经元的LSTM层,第三层为10个神经元的全连接Dense层,输出层为1个神经元的Dense层,用于预测结果的输出,训练过程如下图3-5所示。

建立完神经网络模型后,使用compile函数对网络的学习过程进行参数配置,其中重要参数为优化器、学习率、损失函数和评估函数。接下来使用fit函数进行模型训练,由于数据量并不是特别的大,所以batch_size即每次喂入的数据量初步设为32,epoch即训练次数初步设为300。
3.2.1DropOut
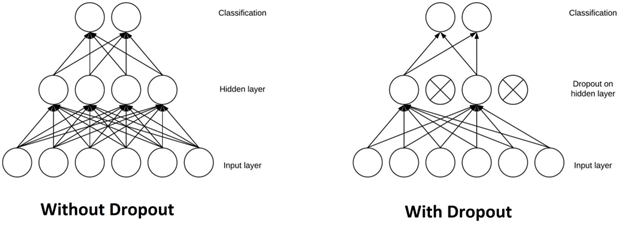
全连接层占据了大部分参数,神经元在训练过程中彼此依赖连接,这抑制了每个神经元的个体能力,导致训练数据存在过拟合的问题。简单地说,DropOut 是指在训练阶段忽略随机选择的一组神经元的单元(即神经元),可以防止网络过度依赖单个神经元,并迫使所有神经元学习更好地泛化,DropOut原理可视化如下图3-6所示[24]。
本文要应用 DropOut,需要为每一层设置保留概率,保留概率指定一个单元被丢弃的概率 。标准做法是将隐藏层的保留概率设置为 0.2-0.5,由于训练过程中容易产生过拟合问题,所以在贵州茅台的初步模型训练中概率 设置为0.1,输出层不应用 DropOut。
3.2.2优化器
深度学习的训练过程中非常重要的一环就是优化函数。神经网络中的损失是由该模型得出的测量结果与实际数据的差异,也是对该模型进行建模的一个重要参数。优化器帮助我们理解怎样在网络中调整权重和学习速度,从而降低损失。
该算法是一种将 Adam算法与 RMSProp相结合的自适应动量随机优化算法,并将其优势与 RMSProp相结合,并将梯度的一阶矩和二阶矩估计相结合,对噪声问题进行了处理。Adam算法的参数有学习率(alpha)、一阶矩估计的指数衰减率(beta1)、二阶矩估计的指数衰减率(beta2)以及epsilon[25]。
在这种情况下,学习速率是影响神经网络权重的一个关键因素,在这种情况下,学习速率是影响神经网络权重的一个关键因素。若学习率过小,梯度下降缓慢,可能导致神经网络到达局部极值就收敛,无法找到最优解。另外三个参数通常使用默认值、无需调整或仅需微调。
在一般情况下,Adam优化算法很适用于LSTM模型,它能找到一系列的参数来最小化LSTM的损失函数,从而提高模型的精准度。
3.2.3损失函数
在最优解的基础上,模型的当前状态误差需要反复估算。这就要求我们选取一种叫做损耗函数的错误函数来估算模型的损耗,从而可以通过修正权重来降低下次估算的损失[26]。
损失函数(Loss Function)又称为代价函数(Cost Function),是把随机事件或相关的随机变量的数值映射成一个非负的实数,用以代表“风险”或“损失”。机器学习的问题一般是通过原始数据、原始模型和原始知识来求解最小损失函数和最优模型。最后用损失函数来构建模型的学习标准和优化问题,一般采用损失函数来判定模型的预测值和真实值之间的差异[27]。
均方误差(MSE,Mean Square Error)是用于回归问题的默认损失。在最大似然性理论中,当输入变量为高斯分布时,该方法是最优的损失函数,所以本文在编译模型时将mean_squared_error作为首选损失函数。均方误差计算为预测值和实际值之间的平方差的平均值。不管预测和真实数值的符号是什么,最终的结果总是积极的,并且是0.0。平方表示较大的误差,较小的误差会造成更多的误差,这意味着模型因犯了较大的错误而受到惩罚。
均方误差MSE计算公式如下:
\begin{equation}
M S E=\frac{1}{m} \sum_{i=1}^{m}\left(f_{i}-y_{i}\right)^{2}
\end{equation}
其中fi是预测值,fi是真实值。MSE越小越好,说明该模型描述实验数据具有更好的精度。MAE的值越接近0,模型的拟合度越好。
3.2.4评价函数
股票预测的任务是预测一个具体的数值,网络输出一般只有一个节点即预测值,在这种情况下为了更好的评估LSTM的预测效果,本文选择经典的平均绝对误差百分比(MAPE,Mean Absolute Percentage Error)、平均绝对误差(MAE,Mean Absolute Error)和 R^2值 ( R^2 ,R-squared)用作方法的评估标准。
平均绝对误差百分比 MAPE 计算公式如下:
\begin{equation}
M A P E=\frac{1}{m} \sum_{i=1}^{m}\left|\frac{f_{i}-y_{i}}{y_{i}}\right|
\end{equation}
MAPE 值越小即越接近0,表示预测结果较真实结果平均偏离越小,预测效果越好。
平均绝对误差 MAE 计算公式如下:
\begin{equation}
M A E=\frac{1}{m} \sum_{i=1}^{m}\left|f_{i}-y_{i}\right|
\end{equation}
MAE越小越好,由于其不能求导,因此 MAE的最优解一般都是用损失函数求导数来进行优化,因此 MAE对离群值的敏感性较低,而对均值和标度则比较敏感。
R方值 R^2计算公式如下:
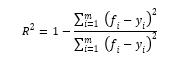
R方值被誉为最好的衡量线性回归法的指标。其中y^是预测值,yi是真实值,y-是平均值。R^2的取值范围为(-∞,1)。R^2越接近1,模型的拟合度越好。
3.3实验以及实验结论分析
3.3.1训练基本模型及预测
首先针对贵州茅台的股票数据信息,输入3442组包含OHLCVM六个特征的训练数据,对建立的LSTM神经网络进行训练。下图展示了随着epoch次数的增加,具体指标 MSE、MAPE、MAE不断趋近于0,而R^2趋近于1,反映了模型迭代过程即梯度下降来不断优化学习的过程。但是当然,初步模型在训练过程中仍然由于参数选择不当,存在极个别训练过程中出现异常模型的问题,其对应训练次数具体亦可由下图3-7所示MSE、MAPE、MAE、R^2 指标中看出。
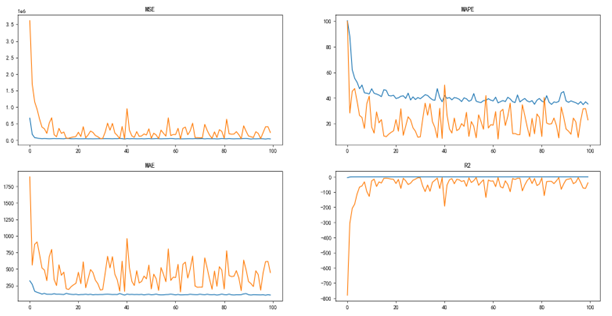
在本次初步实验中我们使用最后一次的模型来进行预测,使用predict方法喂入383组测试数据进行预测,输出测试数据。下图提供了真实数据和预测数据的对比曲线,其中红色曲线为测试集中的真实数据,绿色曲线为对应的预测值。
尽管最后一次的训练模型在训练集和测试集上并不能保证是最优模型,但是其预测趋势还是可观的,由平均绝对误差百分比我们可以验得模型的准确率为 77.03% ,尽管其价格预测准确度上存在较大差距,但是由如下图3-4贵州茅台基本模型可视化所示,其预测趋势仍具有一定的可参考性。

对于另外三支股票(其顺序分别为万科、云南白药和紫光国微,下同)做同样的处理,具体各项参数设置如下表所示。
| parameter | value |
|---|---|
| memory_days | 30 |
| pre_days | 10 |
| learning_rate | 0.001 |
| lstm_layers | 1 |
| dense_layers | 1 |
| units | 100 |
| dropout | 0.1 |
| epoch | 100 |
该三支股票基本模型预测结果对应准确率如下表所示。
| stock | val_acc |
|---|---|
| 贵州茅台 | 77.03% |
| 万科 | 81.88% |
| 云南白药 | 89.01% |
| 紫光国微 | 68.75% |
该三只股票基本模型各项损失评估函数值变化以及模型预测图如下图3-9所示。
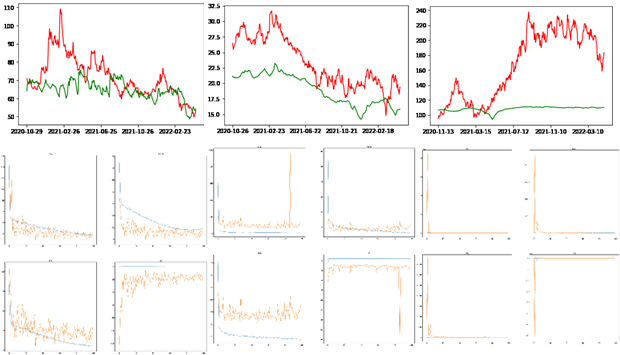
3.3.2模型评估
从贵州茅台、万科、云南白药等预测结果中我们可以看出,本预测模型在对应的每只股票中均可以在短期内达到很好的预测效果,能够在一定程度上帮用户提前认识到 “牛市”、“熊市”的来临,避免损失或者获得一定投资收益。但是紫光国微的模型预测并没有达到同样的理想预期效果,原因是近年来该公司及其芯片领域受政治因素影响较大,再加上当前疫情全球缺芯状态严重,国内芯片投资领域处于混乱状态。但是模型仍然存在可优化提升的空间,仍可以进一步通过多层循环遍历找到最优的参数。
根据 LSTM 网络的参数设置,以贵州茅台股票训练模型分析,我们可以知道具体的模型构造如下:输入的训练集数据是一个三维数据向量(None,30,6),其中30是 memory_days和6是输入维度的6个特征。首先,数据进入LSTM层提取特征,得到一个三维输出向量(None,30,10),其中10是输入层神经元的个数。接下来向量进入隐藏层的第一层LSTM层,同样得到一个三维的输出向量(None,30,80)。然后,输出向量进入隐藏层的第二层LSTM层,输出数据(None,100)训练后进入隐藏层的第三层全连接层,得到的输出值(None,10)进入最后一层全连接层得到输出值(None,1)。具体的贵州茅台股票信息LSTM 的股票预测模型结构如下图3-10所示。
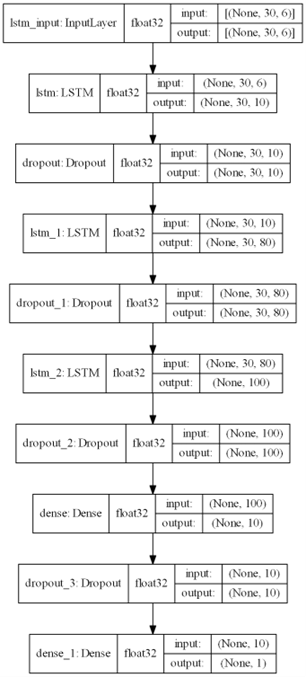
其参数计算如下:
对于lstm层,计算公式为:参数数量 = 4 * ((词向量的维度 + lstm神经元个数) * lstm神经元个数 + lstm神经元个数) 。例如输入层的参数计算可写为 10 *(6+10+1) * 4 = 680,其中第一个10是这一层神经元的个数为10,第二个10是本层神经元的个数,6代表的是上层神经元的返回值,1是指偏移量也就是我们在 2.3.2 中提到的 ReLu 函数,4指的是lstm本身含有的四个参数。同理,其他层的计算过程如下表所示:
| layer(type) | Output Shape | param |
|---|---|---|
| LSTM | (None,30,10) | 10 * ( 6 + 10 + 1 ) * 4 = 680 |
| LSTM | (None,30,80) | 80 * ( 80 + 10 + 1 ) * 4 = 29120 |
| LSTM | (None,100) | 100 * ( 100 + 80 + 1 ) * 4 = 72400 |
| Dense | (None,10) | 10 * ( 100 + 1 ) = 1010 |
| Dense | (None,1) | 1 * ( 10 + 1 ) = 11 |
3.3.3模型优化
但是本次实验我们默认选择最后一次训练的模型为最终预测模型,尽管随着每次训练,无论是损失函数还是评价指标,整体上模型是朝着好的方向变化,但是这并不能保证确定最后一次训练的模型为最优模型。
训练神经网络的一个问题在于选择要使用的训练 epoch 的数量。epoch 太多会导致训练数据集的过度拟合,而太少可能会导致模型欠拟合。提前停止是一种允许您指定任意大量训练时期并在模型性能停止在保留验证数据集上改进时停止训练的方法。Keras提供了Callback函数,提供了一种自动执行代码并与训练模型过程交互的方法。Keras可以在模型训练期间监控其他指标,在编译模型时通过compile 函数的metrics 参数指定。根据性能度量的选择,需要将“模式”参数指定为所选度量的目标是增加(最大化或“最大”)还是减少(最小化或“最小”)。因此本文需要使用callback回调函数,使模型朝着更有利的方向训练优化,并保留住最优的模型,以便后期使用其进行模型的评估和最终的应用预测。
回调一旦触发就会停止训练,但训练结束时的模型可能不是验证数据集上性能最好的模型,这时就需要一个额外的回调来保存训练期间观察到的最佳模型以供以后使用,这就是ModelCheckpoint回调的实现过程。ModelCheckpoint回调的使用方式很灵活,但在这种情况下,我们将仅使用它来保存训练期间观察到的最佳模型,该模型由验证数据集上的所选性能度量定义。
下面以贵州茅台为例进行callback回调函数记录最优模型,使用tensorboard_callback记录损失评价的变化情况,并使用MAPE作为评估指标,力求越小越好来保存模型,如图3-11所示为训练300次,MSE、MSPE、MAE以及R^2随着训练次数的变化曲线,整体趋势如基本模型相似,均表明随着训练次数,模型不断地在朝着好的方向发展。
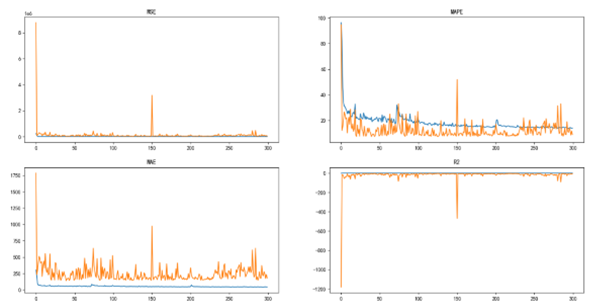
同时,本实验在贵州茅台预测模型的训练中使用CheckPoint模型保存,记录保存了较优模型及其各项指标情况,如下表所示,从各项较优模型的指标上,可以看到尽管只是把MAPE作为回调的度量指标,但是其实在训练过程中,这些较优的模型在其他指标上相比与上一代较优模型均有提高。同时可以得知,尽管本实验设置的epoch为300,但是在模型训练优化上在超过50次后仍没有较大的提升,因此在后续实验上可以考虑其背后的原因。
| epoch | MAPE | MAE | R^2 | MASE |
|---|---|---|---|---|
| 01 | 94.61 | 1784.81 | -1181.6 | 8765998 |
| 02 | 12.08 | 232.86 | -14.44 | 118117.92 |
| 09 | 10.27 | 203.98 | -7.27 | 70766.05 |
| 20 | 8.52 | 170.11 | -4.62 | 50254.89 |
| 21 | 7.43 | 147.04 | -3.2 | 37373.09 |
| 40 | 7.38 | 139.91 | -3.61 | 31213.57 |
| 178 | 7.37 | 142.19 | -3.75 | 31894.38 |
最后本文选择使用第40次训练得到的相对较优模型进行模型评估,由平均绝对误差百分比计算得到的准确率为92.62%,相较于初步模型的77.03%有较大的提升,如其预测可视化曲线图3-12也可以相比于基本模型看出有较大的提升。
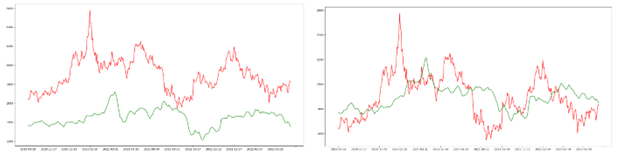
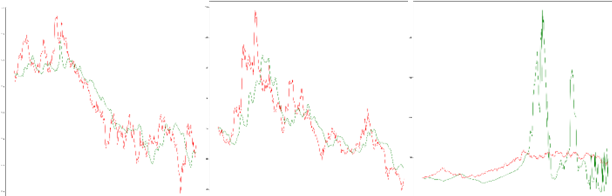
其他三只股票对应的准确率及优化预测结果如下表、图3-13所示:
| stock | basic_val_acc | update_val_acc |
|---|---|---|
| 贵州茅台 | 77.03% | 92.62% |
| 万科 | 81.88% | 93.50% |
| 云南白药 | 89.01% | 93.09% |
| 紫光国微 | 68.75% | 68.76% |
四、模型改进以及训练最优模型
4.1超参数优化分析
网络中的超参数可以划分为网络参数、优化参数和规则化参数。超参数优化,实质上就是寻求最优解与规则项的关系。网络模型优化调整的目标是寻求全局最优或较好的局部最优,而规则项要求模型尽可能地接近最佳。一般来讲,这两种方法都有一些矛盾,但是它们的目的都是使预期危险降到最低。在模型优化中,最大限度地减少了经验风险,同时也使得模型的复杂性受到了限制。因此,如何使二者的关系达到最佳或更好的结果,就成为了超参数调整的目标。
学习率对预测模型的影响:网络参数,优化参数,正则化参数中最关键的因素是学习率(learning rate)。学习速率是权重更新的主要因素,如果设定过大,则导致权重的大小超出最佳,反之,则导致权重的降低。学习速率是指在最优算法中对网络权值进行修正的幅度。学习速率可以是恒定的、递减的、基于动量的或自适应的,而使用的学习速率与所选的最优算法的种类有关,学习速率的大小直接决定了训练网络的梯度更新的数量,并直接决定了模型的有效容限[28]。
神经网络层数对预测模型的影响:神经网络层数(layers)对模型训练的重要性不言而喻,其本质就是模型的深度问题。在相同的情况下,随着模型深度的增大,模型的容量增大,模型的参数越多,拟合的性能也越好,但其缺点是所需的时间和硬件资源较多。在深度学习模型的设计中需要秉持的基本准则是在损失评价函数相对差距不大的情况下,尽量选择较小的层数,这样既保证了训练的模型没有出现过拟合也保证了时间和资源上效率的提高[29]。
神经元数对预测模型的影响:选择适当的隐藏神经元数目非常关键,因为隐藏层中的神经元数目太少会造成不匹配,反之,过度使用也会造成某些问题。由于神经网络节点太多,训练集内的信息数量有限,无法对隐藏层中的所有神经元进行训练,从而产生过度拟合。尽管训练数据中含有大量的信息,但由于隐藏层中的神经元数量太多,导致训练时间延长,很难获得预期的训练结果[30]。
Dropout比率对预测模型的影响:添加 Dropout层是一种常见的正则化方法,它能削弱神经网络的过度拟合作用。该方法会按照所设定的概率参数,在每次训练中随机地不激活该设定值比例的神经单元,适当的丢弃率可以提高模型的容量,而减少的丢弃参数则会提高模型的参数,提高参数之间的适应性,提高模型的容量,该参数比率控制在0.1-0.5[31]。
4.2模型设计
在当前的神经网络超参数调节领域, keras社区已经研制出了Keras-Tuner,超参数可伸缩的最佳化架构。Keras Tuner是一种简易方便、具有分布式结构的超参数优化架构,它可以帮助用户在进行超参搜索时克服困难。Keras Tuner能够轻松地定义一个搜索空间,并且使用该算法找到最优的超参数。Keras Tuner内置了贝叶斯优化(Bayesian Optimization)、Hyperband和随机搜索(Random Search)算法,同时也便于研究人员扩展,进行新搜索算法的试验[32]。
超对象类是一个 hyerparameter容器。一个超级参数实例包含了所有的搜索空间和当前的值。当然,您也可以通过建立一个包含超参数值的模型来建立一个内嵌的超级参数,这将帮助您的代码更加易于维护。
对于紫光国微股票,尽管从基本模型优化得到较好的模型,但是由上面无论是最终模型准确率亦或是预测图像都可以看到模型的提升和模型的预测准确度并没有得到较好的预测,于是接下来本文仅选择针对紫光国微该支股票进行超参数优化,以寻求得到一个较好的升级版模型。首先,定义一个model_builder函数,使用Keras Tuner API进行参数遍历,常用方法有hp.Int、hp.Choice、hp.Float来代替需要调整的超参数,最后使用search函数进行搜索。模型构建工具函数将返回已编译的模型,并使用内嵌方式定义的超参数对模型进行超调。下一步,实例化(instantiate)一个tuner。首先应该指定model-building函数,要优化的目标(objective),要训练的最大周期数(max_epochs)设为3,每次试验模型构建训练次数为10(executions_per_trial)也设为2,其中优化目标是最小化还是最大化是根据内置metrics自动推断出来的,每次试验多次运行的目的是减少结果方差从而可以更精确地获取模型表现。如果想更快地得到结果,可以设置executions_per_trial=1每个模型配置只训练一轮,但是要精度更高肯定要配置更多轮。在贵州茅台的数据模型训练上Keras tuner使用 Hyperband 算法用于超参搜索。可以通过tuner.search_space_summary打印搜索空间综述查看超参数空间,对于紫光国微模型预测的超参数空间如下表所示。
| Hyper Parameters | type | default | range | step |
|---|---|---|---|---|
| units | Int | 32 | [32,512] | 32 |
| drop_p | Float | 0.1 | [0.1,0.5] | 0.1 |
| number_of_lstm | Int | 1 | [1,10] | 1 |
| number_of_dense | Int | 1 | [1,10] | 1 |
| batch_size | Int | 32 | [32,256] | 32 |
| learning_rate | Choice | [1e-2, 1e-3, 1e-4] |
Hyperband调整算法采用了自适应的资源配置和提前停存的方法,以达到高效的模型。这个过程使用了运动竞赛冠军的排除法。该方法在多次训练中对大量的模型进行训练,只有一半的性能最好的模型被投入到下一次的训练中。Hyperband通过将其往上四舍五入到最接近的整数,来决定要训练的模型数目。如果确认损失达到了一个具体的数值,就会建立一个回调来提前终止训练。接下来调用search方法进行超参数搜索,传入预处理的训练集和测试集。search方法与 keras.model.fit 具有相同的参数(signature),因此参数部分,本实验继续选择使用之前基本模型的fit参数信息内容。
4.3模型评估
在超参运算中如果超参设置空间过大的话,仍需要较长的运算时间和资源浪费,但如果过小的话不容易得到较优参数。因此,本实验在超参优化中尽可能地把max_trial和executions_per_trial设为较小的值,经过10轮超参优化并使用results_summary得到输出的超参数结果摘要如下表所示。
| Trail | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
|---|---|---|---|---|---|---|---|---|---|
| val_mape | 37.61 | 45.32 | 47.13 | 56.77 | NaN | NaN | 31.62 | 162.50 | |
| units | 128 | 128 | 32 | 96 | 256 | 384 | 224 | 64 | 256 |
| p | 0.3 | 0.2 | 0.3 | 0.4 | 0.1 | 0.3 | 0.3 | 0.4 | 0.5 |
| the_number_of_lstm | 7 | 7 | 7 | 8 | 1 | 1 | 7 | 1 | 7 |
| the_number_of_dense | 4 | 6 | 6 | 6 | 3 | 10 | 4 | 7 | 2 |
| batch_size | 128 | 256 | 224 | 160 | 224 | 160 | 256 | 160 | 192 |
| learning_rate | 0.0001 | 0.001 | 0.0001 | 0.001 | 0.01 | 0.01 | 0.01 | 0.0001 |
实验部分我们仅将trail#1的参数带入实验,使用callback回调函数和tensorboard查看模型优化性能并进行预测,由最终预测图我们可以得知,此超参数优化后的模型的确相比于基本模型优化上得到了一定的提高,准确率达到了70.53%。但是超参数带来的提升并非很大,因为最终输入的超参数只要在一定最优参数范围内,其模型在不断迭代优化的过程中,神经网络的权重和偏移量都会趋于一定的最优化方向调整。
五、总结与展望
5.1总结
本文根据股票价格数据的时间序列特征,使用LSTM来预测次日股票收盘价以及未来一段时间价格走势,本文完成的工作有:
(1)该文以股票数据的开盘价、最高价、最低价、收盘价、成交量和成交额为输入,充分利用股票数据的时间序列特征,LSTM 用于提取的输入的特征数据构造了基本模型并预测股票的收盘价以及价格走势。
(2)在一定参数优化后,实验结果表明,MSE、MAPE、MAE所有损失量达到最小, 接近1,表明 LSTM 在股票预测上的确具有较大的参考价值。
(3)本文以上证综指相关数据为例对实验结果进行验证。LSTM适用于股票价格的预测,可以为投资者实现投资收益最大化提供相关参考,为人们对金融时间序列数据的研究提供了实践经验的建议。
5.2展望
该模型仅是通过历史数据作为输入数据特征,LSTM使用输入特征来预测未来一天的收盘价格以及未来股票价格趋势。但由于个人当前知识水平和时间上的限制,实验存在一些不足之处,仍存在较大的模型提升空间:
(1)本文仅考虑股价数据对收盘价的影响,未能将新闻、国家政策等情绪因素纳入预测,需要增加股票相关新闻和国家政策的情绪分析,加入更多的数据特征,以保证股票预测的准确性。
(2)该模型可以应用在当前股票金融市场的量化交易上,为机器自动化实现短期收益提供股票购入卖出抉择的判定。
(3)优化后的算法网络结构尽管一定程度上可以为投资者实现投资收益最大化提供相关参考,但是在预测精度和准确率上仍然较低,仍需要进一步优化网络结构和算法。
参考文献
[1] 朱容萱. 股票限价指令簿中间价格趋势预测模型研究[D].大连理工大学,2021.DOI:10.26991/d.cnki.gdllu.2021.001694.
[2] Li J, Pan S, Huang L. A machine learning based method for customer behavior prediction[J]. Tehnički vjesnik, 2019, 26(6): 1670-1676.
[3] White H. Economic prediction using neural networks: The case of IBM daily stock returns[C]//ICNN. 1988, 2: 451-458.
[4] Zhang G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50: 159-175.
[5] Sun Y F, Liang Y C, Zhang W L, et al. Optimal partition algorithm of the RBF neural network and its application to financial time series forecasting[J]. Neural Computing & Applications, 2005, 14(1): 36-44.
[6] Adhikari R, Agrawal R K. A combination of artificial neural network and random walk models for financial time series forecasting[J]. Neural Computing and Applications, 2014, 24(6): 1441-1449.
[7] Zhang L, Wang F, Xu B, et al. Prediction of stock prices based on LM-BP neural network and the estimation of overfitting point by RDCI[J]. Neural Computing and Applications, 2018, 30(5): 1425-1444.
[8] 黄宏运. 一种改进的IPSO-BP神经网络在股指预测中的应用——以上证综指为例[J]. 延边大学学报:自然科学版, 2016, 42(4):6.
[9] Alibašić E, Fažo B, Petrović I. A new approach to calculating electrical energy losses on power lines with a new improved three-mode method[J]. Tehnički vjesnik, 2019, 26(2): 405-411.
[10] Yan X, Weihan W, Chang M. Research on financial assets transaction prediction model based on LSTM neural network[J]. Neural Computing and Applications, 2021, 33(1): 257-270.
[11] 曹晓波. 我国股票市场稳定性影响因素的实证研究[D].西南财经大学,2014.
[12] 付丽丽. 投资者情绪对中国股票收益的影响研究[D].山东大学,2018. 陈泗蓉. 基于循环神经网络模型的不同成熟度市场股指预测[D]. 西南财经大学.
[13] 邢伟琛.大数据环境下的股票预测探究[J].中国商论,2020(03):31-32.DOI:10.19699/j.cnki.issn2096-0298.2020.03.031.
[14] Zaremba W, Sutskever I, Vinyals O. Recurrent neural network regularization[J]. arXiv preprint arXiv:1409.2329, 2014.
[15] Shi X, Chen Z, Wang H, et al. Convolutional LSTM network: A machine learning approach for precipitation nowcasting[J]. Advances in neural information processing systems, 2015, 28.
[16] Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks[C]//Proceedings of the fourteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings, 2011: 315-323.
[17] 谈继勇.深度学习500问[M]. 郭子钊等. 北京:电子工业出版社,2020
[18] 高扬卫峥.白话深度学习与Tensorflow[M]. 万娟等. 北京:机械工业出版社,2017
[19] 杨世林. 基于聚宽量化投资平台的股票多因子策略应用[D]. 浙江大学, 2018.
[20] 唐江萍. 基于现金流视角的上市公司估值探索[D].云南财经大学, ssss2020.
[21] 黄菁菁, 刘晓宇, 张驰. 助力健康中国:云南白药的品牌转型之思[J]. 口腔护理用品工业, 2021, 31(6):6.
[22] 周俊吉. 紫光”从芯到云”战略并购研究——基于紫光国芯,紫光股份视角[D]. 西南财经大学.
[23] 肖梁欢. 万科轻资产转型盈利模式及其财务风险评价研究[D]. 南京师范大学, 2018.
[24] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The journal of machine learning research, 2014, 15(1): 1929-1958.
[25] Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
[26] Wang Q, Ma Y, Zhao K, et al. A comprehensive survey of loss functions in machine learning[J]. Annals of Data Science, 2022, 9(2): 187-212.
[27] 陈怡然廖宁.机器学习从入门到精通[M]. 杨倩等. 西安:西安电子科技大学出版社,2020
[28] Jacobs R A. Increased rates of convergence through learning rate adaptation[J]. Neural networks, 1988, 1(4): 295-307.
[29] Kawaguchi K. On the theory of implicit deep learning: Global convergence with implicit layers[J]. arXiv preprint arXiv:2102.07346, 2021.
[30] Weigend A. On overfitting and the effective number of hidden units[C]//Proceedings of the 1993 connectionist models summer school. 1994, 1: 335-342.
[31] Garbin C, Zhu X, Marques O. Dropout vs. batch normalization: an empirical study of their impact to deep learning[J]. Multimedia Tools and Applications, 2020, 79(19): 12777-12815.
[32] Pon M Z A, KK K P. Hyperparameter tuning of deep learning models in keras[J]. Sparklinglight Transactions on Artificial Intelligence and Quantum Computing (STAIQC), 2021, 1(1): 36-40.
致谢
这一年,我二十二岁,在我一生的黄金时代,完成了大学的学业。大学生活过的很快,快到让我恍惚觉得昨天刚拿着录取通知书入学。大概美好的日子总是这样稍纵即逝。印象派中对于稍纵即逝的美好有一种隐秘的哲学理念。停笔默观,回忆大学四年点点滴滴,历历在目,犹如昨日,彷若大梦初醒。
饮水思其源,成学念吾师。首先我要感谢我的毕业论文指导老师,在我毕业设计过程期间自始至终提供精心的帮助与指导。桃李不言,下自成蹊。其次感谢所有的大一到大四任课老师和所有的行政管理老师,能够在求学生涯中遇到各位恩师,应该是人生的幸运吧。
独学而无友,则孤陋而寡闻。感谢我的朋友和同学舍友们,为我人生画布中留下了最自由潇洒又纯粹的年轻画面,能够与你们相遇在这高密一起学习工作生活是何等地幸运。感谢你们四年里对我的帮助支持与信任,为这平淡的日子添加了不少色彩。愿我们此去前程似锦,归来仍是少年!
我要特别感恩我的父母和家人,他们是我人生画布中最重要的角色。二十年来衣食无忧背后是父母的辛勤劳作和起早贪黑,感谢父母家人对我的支持与照顾。他们从小到大一直对我极度自信和支持,觉得我什么都行,相信我什么都可以做好。这种鼓励给我带来很多的积极影响和信心,培养了我面对生活和事物乐观的心态。陪我在每个关键转折点做出更优的选择,使我更加顺利的度过了学生时代。
最后要感谢的是我自己。感谢那个不愿意辜负自己的期待,积极向上的自己;更感谢那个哪怕面对未知的未来,勇敢做出自己的选择努力考研,并愿意为之拼搏奋斗的自己。君子坐而论道,少年起而行之,相信我会不忘初心,带着所有人的期许秉长空万里。
过往皆序章,未来皆可盼。走过的路,爱过的人,策划过的活动,我们一起笑过,一起哭过,都永存在这个夏天。会者定离,一期一祈。谢谢能够遇见的所有人,谢谢你们赠予我的黄金时刻。
2022年06月于高密