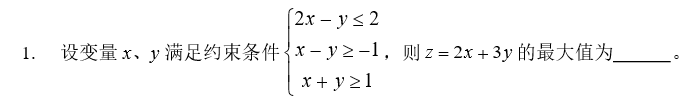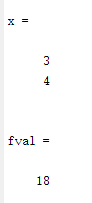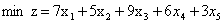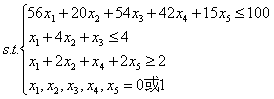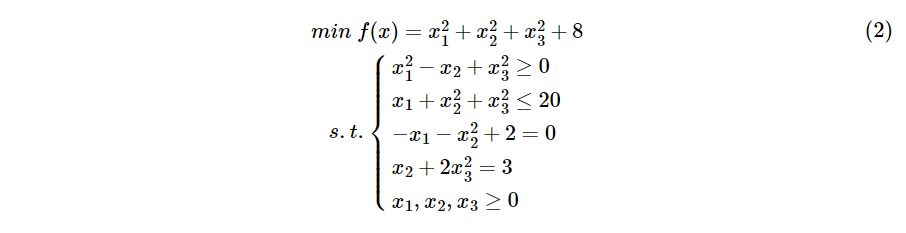matlab学习

一.函数intlinprog的使用

1. intlinprog介绍

intlinprog是matlab中用于求解混合整数线性规划(Mixed-integer linear programming)的一个函数，用法基本和linprog差不多。

intlinprog函数有九个参数

大多数求解线性规划问题时，只用到前面8个参数，所以这里，我就详细的讲解前面8个参数的含义

     f ：目标函数的系数矩阵
intcon ：整数所在位置
     A ：不等式约束的变量系数矩阵
     b ：不等式约束的资源数
   Aeq ：等式约束的变量系数矩阵
   beq ：等式约束的资源数
    lb ：变量约束下限
    ub ：变量约束上限

2. 实例和代码

例1:

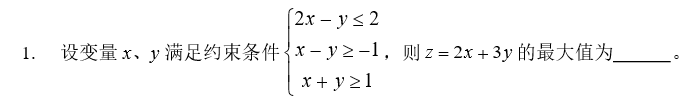
根据函数的使用要求；
求最大值，首先要把目标函数转化为最小值，即min z = - (2x+3y)；
要把大于等于转换为小于等于，即在有 “≥” 符号式子两边同时乘以-1；

代码如下：

f = [-2 -3];                        % 目标函数的系数矩阵
intcon = [];                        % 整数所在位置，题目没有要求，所以是空
A = [2,-1;-1,1;-1,-1];              % 不等式约束的变量系数矩阵
b = [2;1;-1];                       % 不等式约束的资源数
[x,fval] = intlinprog(f,intcon,A,b);    % fval代表最优解处的函数值
x,fval = -fval                      % 返回最大值的结果

运行结果如下；

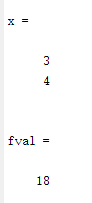
例2:

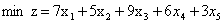
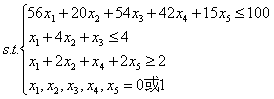
该问题是个0-1规划问题，加上限制条件即可，代码如下：

c = [7 5 9 6 3];
intcon = [1,2,3,4,5];
a = [56,20,54,42,15;1,4,1,0,0;-1,-2,0,-1,-2];
b = [100;4;-2];
aeq=[];
beq=[];
lb = zeros(1,5);        % 生成1×5的 0 矩阵
ub = ones(1,5);         % 生成1×5的 1 矩阵
[x,fval]=intlinprog(c,intcon,a,b,aeq,beq,lb,ub)
%变量的下限是0，上限是1，同时限制了变量是整数。这就是0-1整数规划。同理，其他的规划，可以自己推。

matlab结果如下：
    x =
         0
         0
         0
         0
         1
    fval =
         3

3.补充说明：

使用intlinprog函数时，如果没有该参数所对应的限制条件，是用 [] 符号代替，不可以不写（在不打乱intlinprog函数参数顺序的前提下，如果后面都是[],可以省略不写）

二.函数fmincon的使用

1.简介

在matlab中，fmincon函数可以求解带约束的非线性多变量函数(Constrained nonlinear multivariable function)的最小值,即可以用来求解非线性规划问题
matlab中，非线性规划模型的写法如下

2. 基本语法

[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

参数介绍：

x的返回值是决策向量x的取值，fval的返回值是目标函数f(x)的取值
fun是用M文件定义的函数f(x),代表了(非)线性目标函数
x0是x的初始值
A,b,Aeq,beq定义了线性约束 ,如果没有线性约束，则A=[],b=[],Aeq=[],beq=[]
lb和ub是变量x的下界和上界，如果下界和上界没有约束，则lb=[],ub=[],也可以写成lb的各分量都为 -inf,ub的各分量都为inf
nonlcon是用M文件定义的非线性向量函数约束
options定义了优化参数，不填写表示使用Matlab默认的参数设置

3.实例

求下列非线性规划：

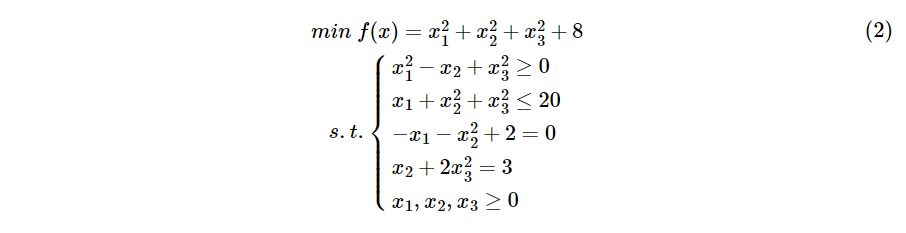
(1)编写fun.m文件存储参数f

1 2	`function f=fun(x) f=x(1)^2+x(2)^2+x(3)^2+8;`

(2)编写nonlcon.m文件

function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^2-20];
ceq=[-x(1)^2-x(2)^2+2
x(2)+2*x(3)^2-3];

(3)执行fmincon()函数

a=[];
b=[];
aeq=[];
beq=[];
lb=zeros(1,3);
ub=[];
[x,val]=fmincon('fun',[0 0 0],a,b,aeq,beq,lb,ub,'nonlcon')

⚠注意事项：

在书写[c,ceq]=nonlcon(x)函数时，c和ceq中若存在$2x_i^2$时，✖需要用 $*$ 表示出来。
$x_0$的值必须要写！
matlab中函数文件名必须要和对应的函数调用时的名字一样。
(4)运行结果
1
2
3
4
x = 0.6312 1.2656 0.9312 val = 10.8672

三.函数fmbnd() fminunc() fminsearch() 与fmincon()

1.求解一元无约束规划

[x, fval]= fminbnd (f,x1,x2）其中fun为目标函数，支持字符串，inline函数，句柄函数，[x1,x2]为优化区间。输出x为最优解，fval为最优值。

1.1 例1 求解一元非线性无约束函数

求函数$y=2e^{-x}sin(x)$在区间【0，8】上的最大值、最小值。

1.1.1 画图

matlab代码如下:
x=0:0.01:8;
y=2*exp(-x).*sin(x);
plot(x,y)

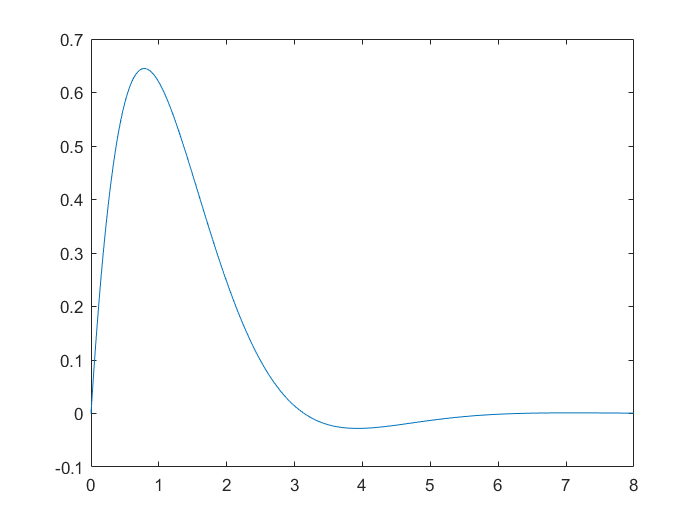
1.1.2 求最大值

代码如下

1 2	`ymax='2exp(-x)sin(x)'; [xmin,fmin]=fminbnd(ymax,0,8)`

答案是

xmin =
        3.9270
fmin =
       -0.0279

1.1.3 求最小值

tip:$fminbnd(y,start,end)$函数默认是求函数$y$的最大值，所以求最小值时我们需要将y函数变号。
matlab代码如下

1 2	`ymin='-2exp(-x)sin(x)' [xmax,fmax]=fminbnd(ymin,0,8)`

答案是

xmax =
        0.7854
    fmax =
       -0.6448

2 多元无约束优化

[x, fval]= fminunc(fun,x0)
[x, fval]= fminsearch(fun,x0)

其中：输入参数fun为目标函数，支持字符串，inline函数、句柄函数，x0为初值，必须得有
注意：fminunc，fminsearch只支持函数fun自变量单变量符号，如x(1),x(2)等

2.1 例2 求解多元非线性无约束函数

$$min \ z=100(x-y^2)^2+(1-y)^2$$

2.1.1 画图

x=-1000:1:1000;
y=x;
z=100(x-y.^2).^2+(1-y).^2;
plot3(x,y,z)

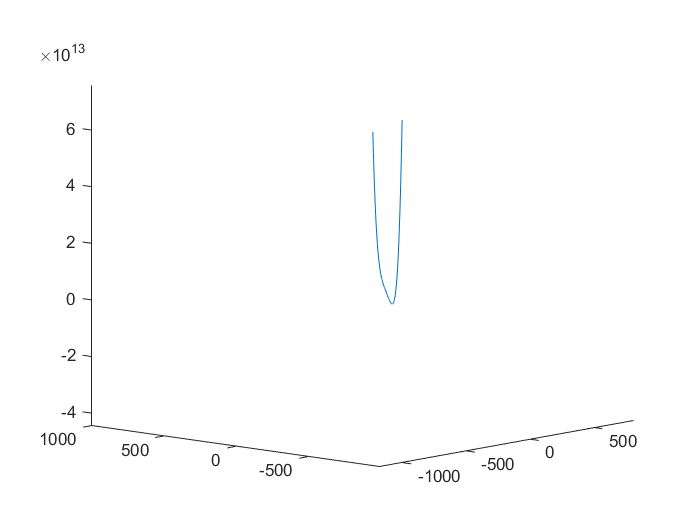
2.1.2 求解最小值

matlab代码如下：

1
2
3

f='100*(x(1)-x(2)^2)^2+(1-x(2))^2';
[x,fval]=fminunc(f,[0,0])
[x_1,fval_1]=fminsearch(f,[0,0])

答案是

x =
        1.0000    1.0000
fval =
       1.9474e-11
x_1 =
        1.0000    1.0000
fval_1 =
       3.6862e-10

2.1.3 区别

我们可以看到上面的结果是不同的，我们可以大胆猜一下可能是每个方法实现的算法不同。

知乎：fminunc与fminsearch函数的区别是什么?
两个都是求极小值，有区别吗？
张国王中科院人工智能研究人员，主攻大规模遥感图像智能化解译
共同点：
算法属性：局部最优化算法
适用范围：无约束多变量最优化问题
不同点：两个函数使用的方法不一样
fminunc 采用拟牛顿法(QN)，是一种使用导数的算法。参见拟牛顿法分析与推导
fminsearch 采用Nelder-Mead单纯形法，是一种直接搜索法。参考单纯形法、Simplex Method

3.有约束优化

这就是我们前几天一直做的问题。
[x, fval]= fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
参数解释:fun为目标函数，支持字符串、inline函数，句柄函数，x0初值，A线性不等式约束系数、b线性不等式约束常数项、Aeq线性等式约束系数，线性beq等式约束常数，nonlcon非线性约束，支持句柄函数。

3.1 例3 求解非线性有约束函数

$$min \ f =x_1^2+4x_2^2+x_3^2$$
$$s.t. \ 3x_1+4x_2+x_3\geq13$$
$$x_1^2+x_2^2-x_3\leq100$$
$$3x_1^2+x_2^2-10\sqrt{x_3}\geq20$$
$$3x_1-x_2^2+x_3=50$$
$$x_1,x_2,x_3\geq0$$

3.1.1 画图

3.1.2 求最小值

matlab代码如下

%(1)编写fun.m函数
function f=fun(x)
f=x(1).^2+4*(2).^2+x(3).^2
%(2)编写nonlcon.m函数
function [c,ceq]=nonlcon(x)
c=[x(1).^2+x(2).^2-x(3)-100
  -3*x(1).^3-x(2).^2+10*x(3).^0.5+20]
  ceq=[3*x(1)-x(2).^2+x(3)-50]
%(3)执行matlab
x0=zeros(1,3)
a=[-3 -4 -1]
b=[-13]
aeq=[]
beq=[]
lb=zeros(1,3)
ub=[]
[x,val]=fmincon('fun',x0,a,b,aeq,beq,lb,ub,'nonlcon')

答案是

x =
       10.8390    0.0005   17.4831
val =
      439.1423

四.关于统计学的一些函数

1. 标准正态分布

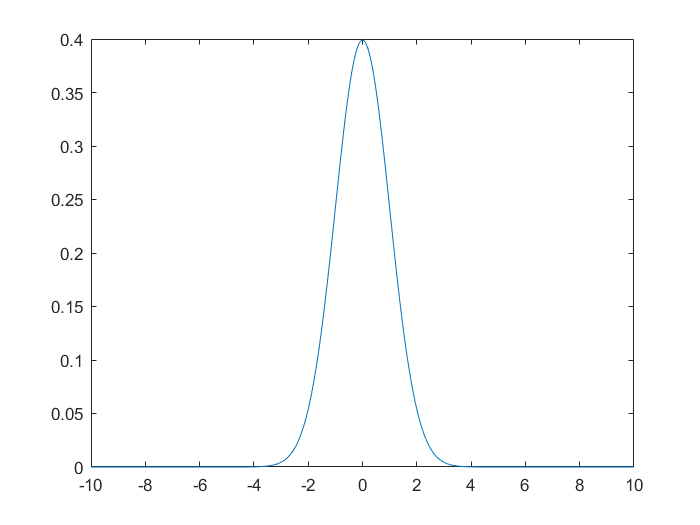
1.1 概率密度函数图像

$$y=normpdf(x,mu,sigma)$$

1.1.1 参数说明

1
2
3

mu：均值
sigma：标准差
y：正态概率密度函数在x处的值

1.1.2 例1

绘制标准正态分布的概率密度图像。

x=-10:0.01:10
mu=0
sigma=1
y=normpdf(x,mu,sigma)
plot(x,y)

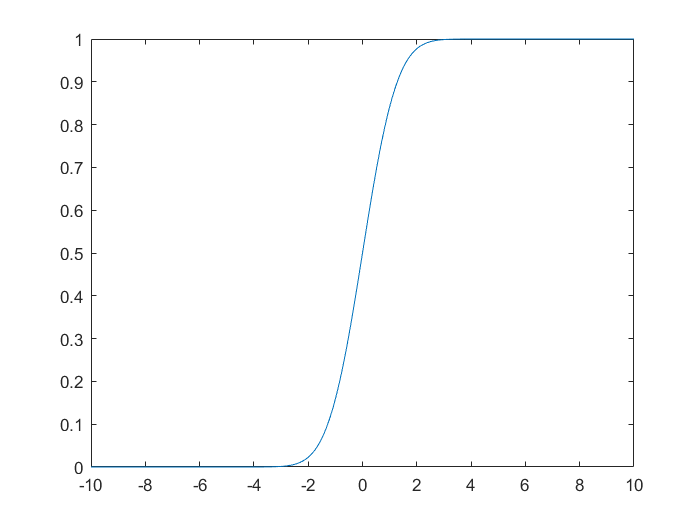
1.2 分布函数图像

$$y=normcdf(x,mu,signma)$$

1.2.1 参数说明

1
2
3

mu：均值
sigma：标准差
y：正态概率函数在x处的值

1.2.2 例2

绘制标准正态分布的分布函数图像。

x=-10:0.01:10
mu=0
sigma=1
y=normcdf(x,mu,sigma)
plot(x,y)

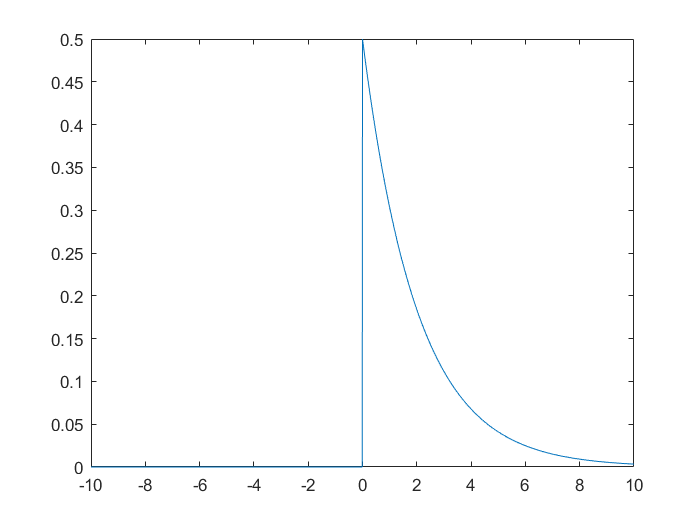
1.3 标准正态分布求分位数

概率密度函数求分位数：

$$norminv(α,mu,sigma)$$

概率分布函数求分位数：

$$norcdf(α,mu,sigma)$$

1.3.1 参数说明

1
2
3

mu：均值
sigma：标准差
ans：α的分位数（即横坐标上的值）

1.3.2 求解标准正态分布α=0.5的分位数

mu=0
sigma=1
norminv(0.5,mu,sigma)
normcdf(0.5,mu,sigma)

答案是

ans =
         0
ans =
        0.6915

2. 卡方分布

2.1 概率密度函数图像

$$y=chi2pdf(x,n)$$

2.1.1 参数说明

1 2	`n：卡方分布的自由度 y：卡方概率密度函数在x处的值`

1.1.2 例1

绘制自由度n=2的卡方分布的概率密度图像。

x=-10:0.01:10
n=2
y=chi2pdf(x,2)
plot(x,y)

2.2 分布函数图像

$$y=chi2cdf(x,n)$$

2.2.1 参数说明

1 2	`n：卡方分布的自由度 y：卡方概率分布函数在x处的值`

1.1.2 例1

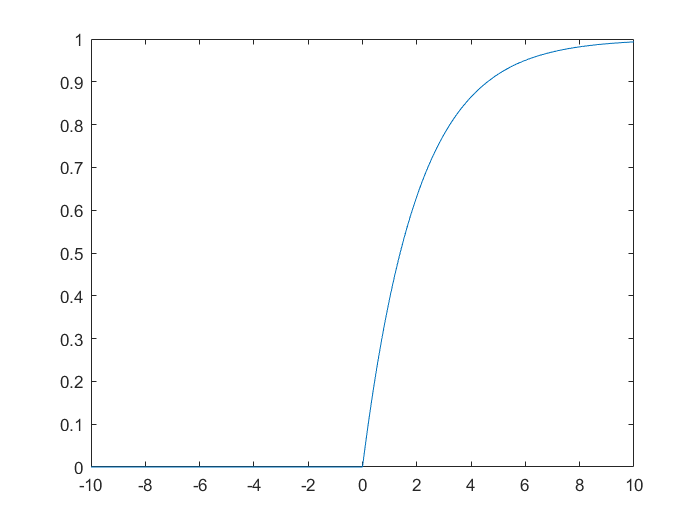
绘制自由度n=2的卡方分布的概率分布图像。

x=-10:0.01:10
n=2
y=chi2cdf(x,2)
plot(x,y)

2.3 卡方分布求分位数

概率密度函数求分位数：

$$chi2inv(α,n)$$

概率分布函数求分位数：

$$chi2cdf(α,n)$$

2.3.1 参数说明

1 2	`n：卡方分布的自由度 ans：α的分位数（即横坐标上的值）`

2.3.2 求解标准正态分布α=0.5的分位数

1
2
3

n=2
chi2inv(0.5,n)
chi2cdf(0.5,n)

答案是

ans =
        1.3863
ans =
        0.2212

3.K-S检验

3.1 正态分布的K-S检验

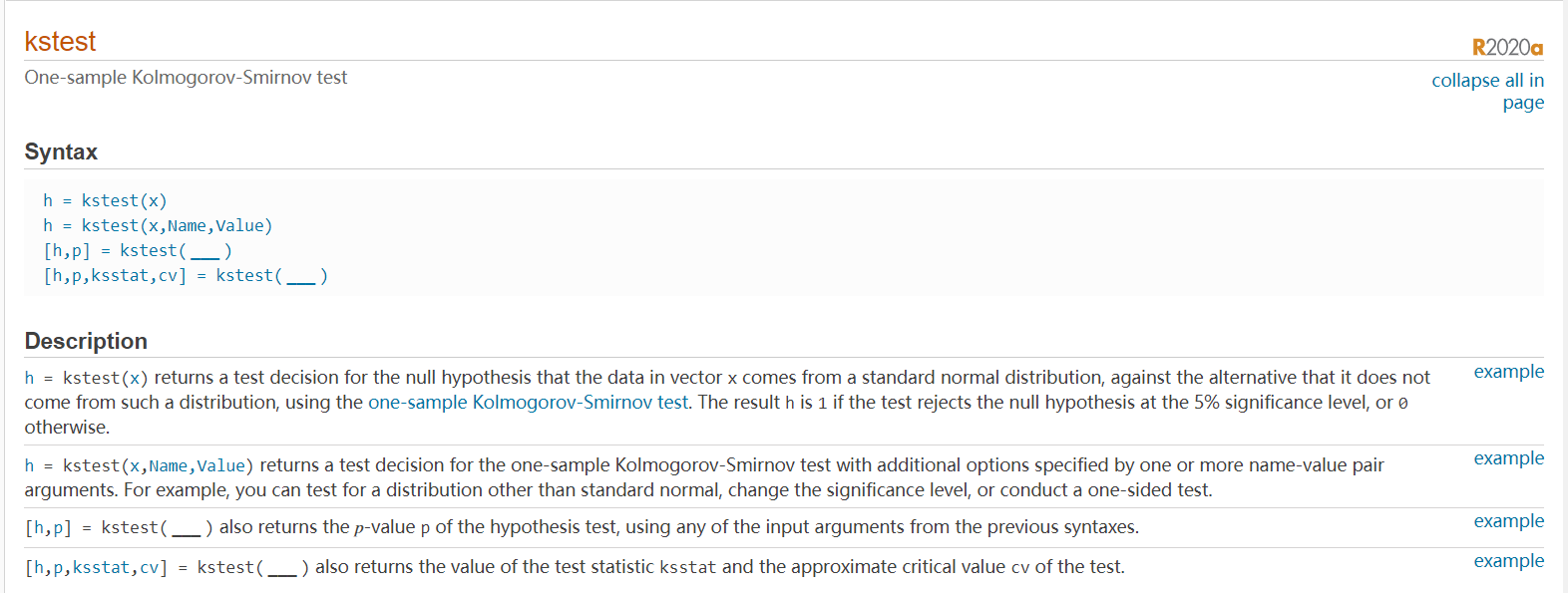
$$H = kstest(X)$$

1	`测试向量X是否服从标准正态分布，测试水平为 5%。`

$$H = kstest(X,cdf)$$

1	`指定累积分布函数为cdf的测试(cdf=[ ]时表示标准正态分布)，测试水平为5%`

$$H = kstest(X,cdf,alpha)$$

1	`alpha为指定测试水平`

$$H=kstest(X,cdf,alpha,tail) $$

1	`tail=0为双侧检验, tail=1单侧(<)检验， tail=-1单侧(>) 检验`

$$[H,P,KSSTAT,CV] = kstest(X,cdf,alpha)$$

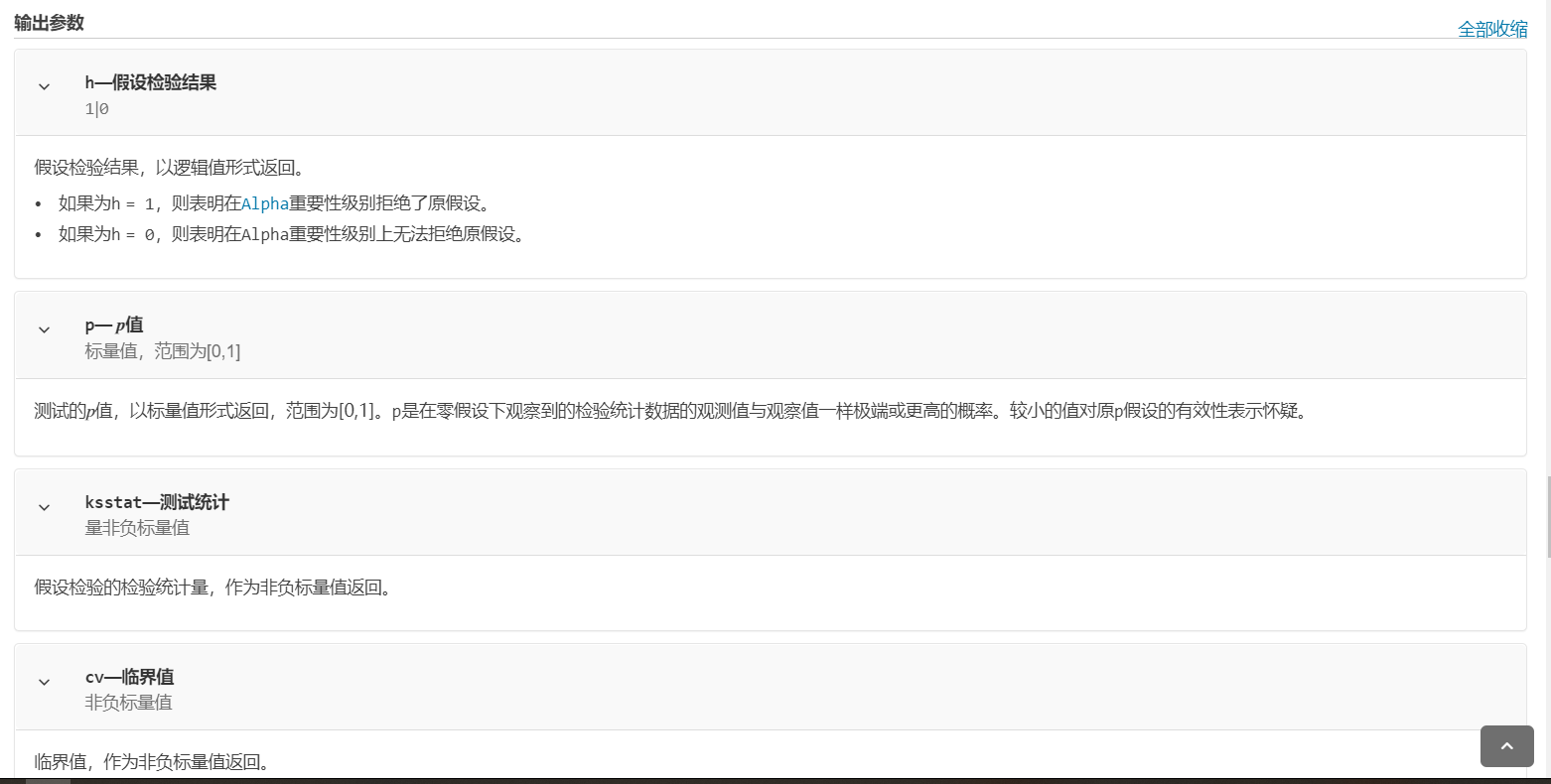
P为原假设成立的概率;
KSSTAT为测试统计量的值;
CV为是否接受假设的临界值。

#### 3.2 其他分布的K-S检验

![QQ图片20200727181059](https://s1.ax1x.com/2020/07/27/aFitHI.png)

#### 3.3 其他检验方法

lillietest检测方法较为严格，容错率低，但参数少。
> chi2gof适合大样本，一般要求50个以上
>   kstest适于小样本，
>   lillietest用于正态分布，与kstest类似，适用于小样本
>   jbtest,是通过峰度、偏度检测正态分布的，适用用大样本。

### 4. 求解分布函数置信区间

![20200727164241](https://s1.ax1x.com/2020/07/27/aFiaUP.png)

### 5.参考文章

[^1]: [matlab中kstest用法详解](https://blog.csdn.net/WUDIPIPIXIA/article/details/101939085)
[^2]: [kstest官方文档](https://ww2.mathworks.cn/help/stats/kstest.html?s_tid=srchtitle)

## 五.函数adftest()

### 1. 函数调用

$h = adftest(x)$
$[h,pValue,stat,cValue,reg] = adftest(x) $

### 2. 功能介绍

**检验时间序列的稳定性。**
h = adftest(x)通过对单变量时间序列中的单位根进行增强的Dickey-Fuller测试来返回具有拒绝决策的逻辑值Y。

### 3. 参数介绍

```shell
h—测试拒绝决策(符合逻辑| 逻辑向量)
测试拒绝决策，以逻辑值或逻辑值向量的形式返回，其长度等于执行的测试次数。
* h = 1 表示拒绝使用单位根null表示支持替代模型。
* h = 0 表示无法拒绝单位根null。

pValue—测试统计p值(标量| 向量)
测试统计p值，以标量或向量的形式返回，其长度等于执行的测试次数。

* 如果检验统计量为't1'或't2'，则p值为左尾概率。

* 如果检验统计量为'F'，则p值为右尾概率。

stat—统计检验(标量| 向量)

测试统计信息，以标量或向量的形式返回，其长度等于执行的测试次数。adftest使用替代模型中系数的普通最小二乘（OLS）估计来计算测试统计量。

cValue—临界值(标量| 向量)

临界值，以标量或向量的形式返回，长度等于执行的测试次数。

* 如果测试统计量为't1'或't2'，则临界值针对左尾概率。

* 如果检验统计量为'F'，则临界值适用于右尾概率。

x— 单变量时间序列(单变量时间序列，指定为列向量。最后一个元素是最近的观察。adftest忽略由NaNs 表示的缺失观测值。)

4. 例

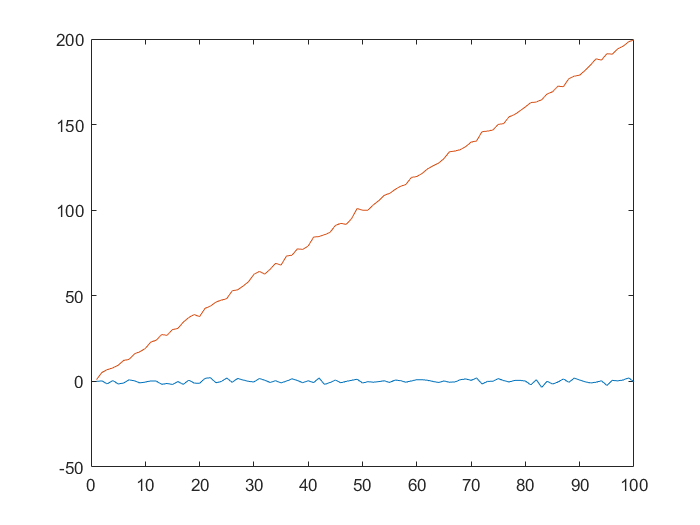
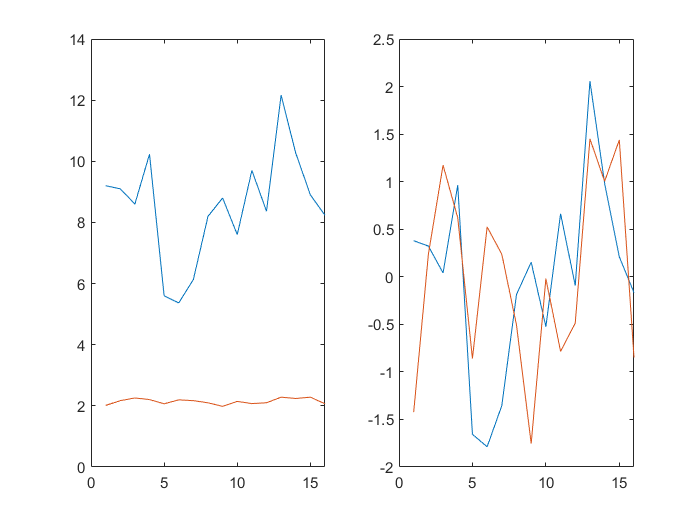
4.1 绘制y1,y2数据时序图

t=(1:100)'
y1=randn(100,1)
y2=randn(100,1)+2*t
plot(t,y1,t,y2)

4.2 绘制y1,y2自相关图像

t=(1:100)'
y1=randn(100,1)
y2=randn(100,1)+2*t
subplot(1,2,1)
autocorr(y1)
xlabel('t')
ylabel('y1')
title('y1自相关图像')
subplot(1,2,2)
autocorr(y2)
xlabel('t')
ylabel('y2')
title('y2自相关图像')

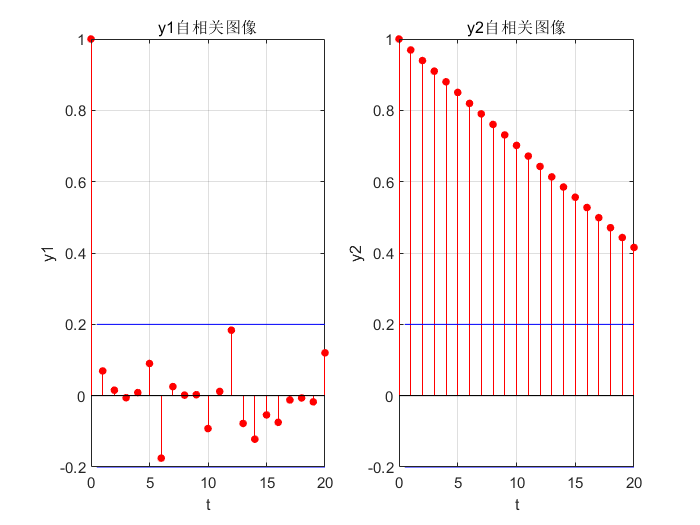
4.3 用adftest求解稳定性

t=(1:100)'
y1=randn(100,1)
y2=randn(100,1)+2*t
plot(t,y1,t,y2)
[h,p,s,cv]=adftest(y1)
[h,p,s,cv]=adftest(y2)

答案是

h =
   logical
   1
p =
   1.0000e-03
s =
   -10.6932
cv =
    -1.9444
h =
   logical
    0
p =
   0.9990
s =
    8.8428
cv =
    -1.9444

五.函数eig() eigs()

1.异同点

1.1 相同点

1	`都可以求解矩阵的特征值和特征向量`

1.2 不同点

1 2	`eig函数主要是给出矩阵的特征值和特征向量 eigs函数主要是通过迭代法来求解矩阵特征值和特征向量`

2.函数语法

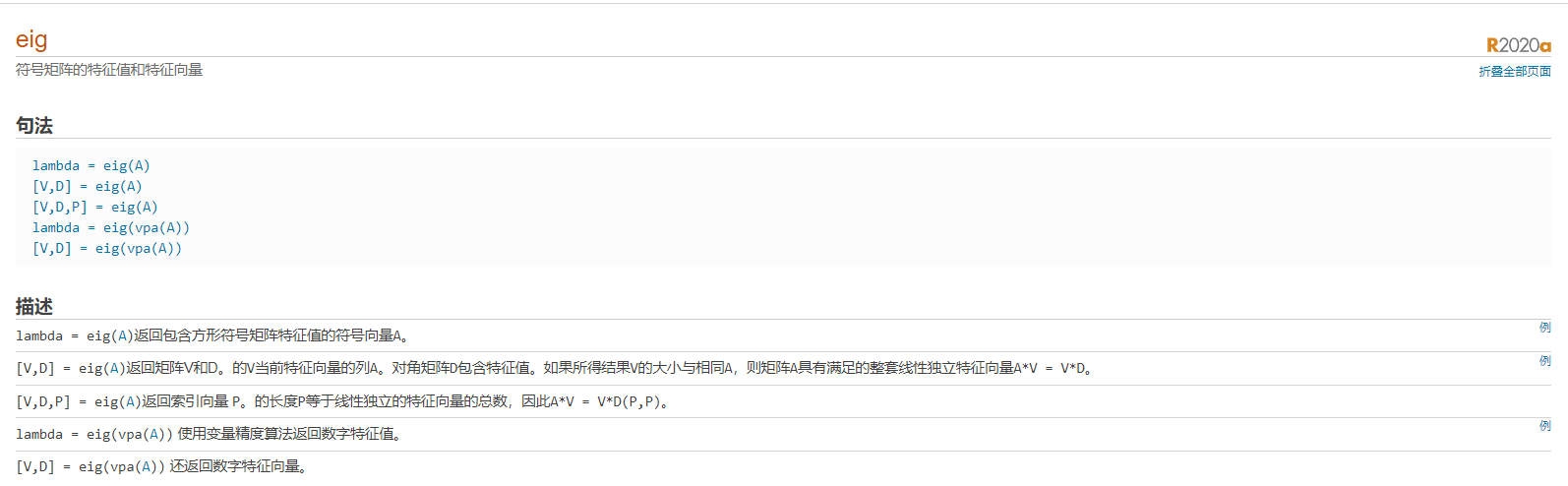
$lambda = eig(A)$

$[V,D] = eig(A)$

$[V,D,P] = eig(A)$

$lambda = eig(vpa(A))$

$[V,D] = eig(vpa(A))$

3. 描述

lambda = eig(A)返回包含方形符号矩阵特征值的符号向量A。
[V,D] = eig(A)返回矩阵V和D。的V当前特征向量的列A。对角矩阵D包含特征值。如果所得结果V的大小与相同A，则矩阵A具有满足的整套线性独立特征向量A*V = V*D。
[V,D,P] = eig(A)返回索引向量 P。的长度P等于线性独立的特征向量的总数，因此A*V = V*D(P,P)。
lambda = eig(vpa(A)) 使用变量精度算法返回数字特征值。
[V,D] = eig(vpa(A)) 还返回数字特征向量。

4.输入参数

1	`A— 矩阵，指定为符号矩阵。`

5.例

1
2
3

A=[-2 1 1;0 2 0;-4 1 3]
[v,d]=eig(A)
[v,d]=eigs(A)

结果是：
    v =
       -0.7071   -0.2425    0.3015
             0         0    0.9045
       -0.7071   -0.9701    0.3015
    d =
        -1     0     0
         0     2     0
         0     0     2
    v =
       -0.2425    0.3015   -0.7071
             0    0.9045         0
       -0.9701    0.3015   -0.7071
    d =
         2     0     0
         0     2     0
         0     0    -1

六.内联函数、匿名函数和函数函数

题目相关链接

1. 字符串函数

1 2	`s='x(1)^2+x(2)^2+8' f=sym(s)`

2. 字符串转化为内联函数

可类似于写在html文件的css样式

s='x(1)^2+x(2)^2+8'
f=inline(s)
x=[8 9]
f(x)

3. 字符串转化为匿名函数

直接转化为匿名函数，直接调用

1
2
3

s='x(1)^2+x(2)^2+8'
x=[8 9]
f=eval(s)

4. 字符串转化为句柄函数

需编写function.m函数并调用函数

function f=fun(x)
f=x(1)^2+x(2)^2+8;
end
%调用规则：
x=[8 9]
fun(x)

七.函数fprintf()

将数据写入文本文件

1.句法

$fprintf(fileID,formatSpec,A1,…,An)$
$fprintf(formatSpec,A1,…,An)$
$nbytes = fprintf( )$

2.描述

fprintf(fileID,formatSpec,A1,…,An)按列顺序将应用于formatSpec数组的所有元素A1,…An，并将数据写入文本文件。fprintf使用对的调用中指定的编码方案fopen。
fprintf(formatSpec,A1,…,An) 格式化数据并在屏幕上显示结果。
nbytes = fprintf(___)fprintf使用前面语法中的任何输入参数，返回写入的字节数。

3.输入参数

fileID— 文件标识符
1（默认）| 2| 标量
formatSpec— 输出字段
格式的格式运算符
A1,…,An— 数字或字符数组
标量 | 向量 | 矩阵 | 多维数组

4.输出参数

nbytes— 标量的字节数

5.例

打印文字文本和数组值

在屏幕上打印多个数值和文字文本。

A1 = [9.9，9900];
A2 = [8.8，7.7; ...
      8800，7700];
formatSpec = 'X为％4.2f米或％8.3f毫米\ n' ;
fprintf（formatSpec，A1，A2）
X是9.90米或9900.000毫米
X是8.80米或8800.000毫米
X是7.70米或7700.000毫米

%4.2f在formatSpec输入规定，在输出的每一行的第一个值是与四位数字，包括小数点后两位数字的字段宽度的浮点数。%8.3f在formatSpec输入规定，在输出的每一行的第二个值是具有8位，包括小数点后三位数字的字段宽度的浮点数。\n是开始新行的控制字符。

将双精度值打印为整数

将带分数的双精度值显式转换为整数值。

a = [1.02 3.04 5.06];
fprintf（'％d \ n'，round（a））;
1个
3
5

%d在formatSpec输入中，将向量中的每个值打印round(a)为有符号整数。\n是开始新行的控制字符。

将表格数据写入文本文件

将指数函数的简短表写入名为的文本文件exp.txt。

x = 0：.1：1;
A = [x; exp（x）];
fileID = fopen（'exp.txt'，'w'）;
fprintf（fileID，'％6s％12s \ n'，'x'，'exp（x）'）;
fprintf（fileID，'％6.2f％12.8f \ n'，A）;
fclose（fileID）;

到第一个呼叫fprintf打印头文本x和exp(x)，并且所述第二呼叫从可变打印中的值A。
如果您打算读取该文件的Microsoft ®记事本，使用’\r\n’，而不是’\n’移动到一个新行。例如，将调用替换fprintf为以下内容：

1 2	`fprintf（fileID，'％6s％12s \ r \ n'，'x'，'exp（x）'）; fprintf（fileID，'％6.2f％12.8f \ r \ n'，A）;`

MATLAB ®导入功能，所有的UNIX ®应用程序，和微软的Word和写字板识别’\n’为一个换行符指标。

使用type命令查看文件的内容。

1	`输入exp.txt`

x exp（x）

0.00 1.00000000
0.10 1.10517092
0.20 1.22140276
0.30 1.34985881
0.40 1.49182470
0.50 1.64872127
0.60 1.82211880
0.70 2.01375271
0.80 2.22554093
0.90 2.45960311
1.00 2.71828183

获取写入文件的字节数

将数据写入文件并返回写入的字节数。
将数据数组写入A文件，并获取fprintf写入的字节数。

1
2
3

A =魔法（4）;
fileID = fopen（'myfile.txt'，'w'）;
nbytes = fprintf（fileID，'％5d％5d％5d％5d \ n'，A）

字节= 96
该fprintf函数将96字节写入文件。
关闭文件。

1	`fclose（fileID）;`

使用type命令查看文件的内容。

1	`类型（'myfile.txt'）`

在命令窗口中显示超链接

在屏幕上显示超链接（MathWorks网站）。

url = 'https://www.mathworks.com' ;
sitename = 'The MathWorks网站' ;
fprintf（'[％s ](%s) \ n'，网址，站点名称）
%s在formatSpec输入指示变量的值url和sitename，应打印为文本。

八.数学上的常见基本函数[1]

1.绝对值和复数幅度

语法

$$Y = abs(X)$$

2.取模

除法（模运算）之后的余数。

语法

$$Y = mod(X)$$

例

>> mod(5,2)
ans =1                   %“除数”是正，“余数”就是正
>> mod(-5,2)
ans =1
>> mod(5,-2)
ans =-1                  %“除数”是负，“余数‘就是负
>> mod(-5,-2)
ans =-1                  %用rem时，不管“除数”是正是负，“余数”的符号与“被除数”的符号相同

3.取余

除后余数。

语法

$$Y = rem(X)$$

>> rem(5,2)
ans =1                   %“被除数”是正，“余数”就是正
>> rem(5,-2)
ans =1
>> rem(-5,2)
ans =-1                 %“被除数”是负，“余数”就是负
>> rem(-5,-2)
ans =-1

4.高斯取整函数

向零舍入。

语法

$$Y = fix(x)$$

例

1
2
3

fix([2.4,3.7,-1.4,-4.7])
ans =
    2     3    -1    -4

5.四舍五入函数

四舍五入到最接近的十进制或整数.

$$Y = round(x)$$

例

1
2
3

round([2.4,3.7,-1.4,-4.7])
ans =
   2     4    -1    -5

6.返回不大于x的最大整数值

向负无穷大舍入。

$$Y = floor(x)$$

例

1
2
3

floor([2.4,3.7,-1.4,-4.7])
ans =
         2     3    -2    -5

7.返回不小于x的最小整数值

向正无穷大方向舍入.

$$Y = ceil(x)$$

例

1
2
3

ceil([2.4,3.7,-1.4,-4.7])
ans =
    3     4    -1    -4

九.format()函数

data1.txt:
    0 3886.162 2200.938 141.240
    1 3721.139 2208.475 141.152
    2 3866.200 2198.936 141.126
    3 3678.048 2199.191 141.250
    4 3685.453 2203.726 141.241

读取数据：
data=load('data1.txt')
dat1 =
    1.0e+03 *
             0    3.8862    2.2009    0.1412
        0.0010    3.7211    2.2085    0.1412
        0.0020    3.8662    2.1989    0.1411
        0.0030    3.6780    2.1992    0.1412
        0.0040    3.6855    2.2037    0.1412

1.format short：默认格式，小数点后保留4位

dat1 =
       1.0e+03 *
             0    3.8862    2.2009    0.1412
        0.0010    3.7211    2.2085    0.1412
        0.0020    3.8662    2.1989    0.1411
        0.0030    3.6780    2.1992    0.1412
        0.0040    3.6855    2.2037    0.1412

2.format long：有效数字16位

dat1 =
       1.0e+03 *
      列 1 至 3
                       0   3.886162000000000   2.200938000000000
       0.001000000000000   3.721139000000000   2.208475000000000
       0.002000000000000   3.866200000000000   2.198936000000000
       0.003000000000000   3.678048000000000   2.199191000000000
       0.004000000000000   3.685453000000000   2.203726000000000
      列 4
       0.141240000000000
       0.141152000000000
       0.141126000000000
       0.141250000000000
       0.141241000000000

3.format long e：有效数字16位加3位指数

dat1 =
      列 1 至 2
                             0     3.886162000000000e+03
         1.000000000000000e+00     3.721139000000000e+03
         2.000000000000000e+00     3.866200000000000e+03
         3.000000000000000e+00     3.678048000000000e+03
         4.000000000000000e+00     3.685453000000000e+03
      列 3 至 4
         2.200938000000000e+03     1.412400000000000e+02
         2.208475000000000e+03     1.411520000000000e+02
         2.198936000000000e+03     1.411260000000000e+02
         2.199191000000000e+03     1.412500000000000e+02
         2.203726000000000e+03     1.412410000000000e+02

4.format short e：有效数字5位加3位指数

dat1 =
                0   3.8862e+03   2.2009e+03   1.4124e+02
       1.0000e+00   3.7211e+03   2.2085e+03   1.4115e+02
       2.0000e+00   3.8662e+03   2.1989e+03   1.4113e+02
       3.0000e+00   3.6780e+03   2.1992e+03   1.4125e+02
       4.0000e+00   3.6855e+03   2.2037e+03   1.4124e+02

5.format bank：保留两位小数位

dat1 =
                 0       3886.16       2200.94        141.24
              1.00       3721.14       2208.47        141.15
              2.00       3866.20       2198.94        141.13
              3.00       3678.05       2199.19        141.25
              4.00       3685.45       2203.73        141.24

6.format +：只给出正负

dat1 =
     +++
    ++++
    ++++
    ++++
    ++++

7.format rational：以分数的形式表示

dat1 =
           0         143788/37       35215/16        3531/25
           1         133961/36       41961/19       17644/125
           2          19331/5        35183/16       17923/127
           3          77239/21       46183/21         565/4
           4          40540/11       24241/11       11723/83

8.format hex：以16进制数表示

dat1 =
      列 1 至 3
       0000000000000000   40ae5c52f1a9fbe7   40a131e04189374c
       3ff0000000000000   40ad12472b020c4a   40a140f333333333
       4000000000000000   40ae346666666666   40a12ddf3b645a1d
       4008000000000000   40acbc189374bc6a   40a12e61cac08312
       4010000000000000   40accae7ef9db22d   40a13773b645a1cb
      列 4
       4061a7ae147ae148
       4061a4dd2f1a9fbe
       4061a4083126e979
       4061a80000000000
       4061a7b645a1cac1

9.format long g：15位有效数

dat1 =
      列 1 至 2
                             0                  3886.162
                             1                  3721.139
                             2                    3866.2
                             3                  3678.048
                             4                  3685.453
      列 3 至 4
                      2200.938                    141.24
                      2208.475                   141.152
                      2198.936                   141.126
                      2199.191                    141.25
                      2203.726                   141.241

10.format short g：5位有效数

dat1 =
                0       3886.2       2200.9       141.24
                1       3721.1       2208.5       141.15
                2       3866.2       2198.9       141.13
                3         3678       2199.2       141.25
                4       3685.5       2203.7       141.24

十.数据文件读取

1.text文件

data1.txt:
    0 3886.162 2200.938 141.240
     1 3721.139 2208.475 141.152
     2 3866.200 2198.936 141.126
     3 3678.048 2199.191 141.250
     4 3685.453 2203.726 141.241

1.dat1=load()

dat1=load('data1.txt')
    dat1 =
       1.0e+03 *
             0    3.8862    2.2009    0.1412
        0.0010    3.7211    2.2085    0.1412
        0.0020    3.8662    2.1989    0.1411
        0.0030    3.6780    2.1992    0.1412
        0.0040    3.6855    2.2037    0.1412

2.dat2=importdata()

dat2=importdata('data1.txt')

dat2 =
      列 1 至 2
                             0                  3886.162
                             1                  3721.139
                             2                    3866.2
                             3                  3678.048
                             4                  3685.453
      列 3 至 4
                      2200.938                    141.24

3.[a,b,c,d]=textread()

[a,b,c,d]=textread('data1.txt','%2d %8.3f %8.3f %7.3f')

a =
         0
         1
         2
         3
         4
b =
                      3886.162
                      3721.139
                        3866.2
                      3678.048
                      3685.453
c =
                      2200.938
                      2208.475
                      2198.936
                      2199.191
                      2203.726
d =
                        141.24
                       141.152
                       141.126
                        141.25
                       141.241

4.dat3=dat2(m:n,p:q)%提取矩阵的指定行和列组成的新矩阵

dat2(1:2,1:2)%提取矩阵的指定行和列组成的新矩阵
ans =
                             0                  3886.162
                             1                  3721.139

2. excel文件

1.num=xlsread(文件名)

num=xlsread('移动通知户开户数.xlsx')
num =
               1       57286
               2       34096
               …………………………………………

2.num=xlsread(文件名,shett号，范围1)

num=xlsread('移动通知户开户数.xlsx','A2:A67')
    num =
         1
         2
         ……

3.num=xlsread(文件名,sheet号)

num=xlsread('移动通知户开户数.xlsx',1)
    num =
               1       57286
               2       34096
               …………………………………………

4.[x,y]=xlsread(文件名,shett号，范围1)

num=xlsread('移动通知户开户数.xlsx',1,'A2:A67')
    num =
         1
         2
         ……

5.num=readtable(文件名)

得到的是table类型数据

1	`num=readtable('移动通知户开户数.xlsx')`

num =
      731×2 table
      Var1    Var2
      ____    _____
       1     57286
       2     34096
       3     26996
       4     29552
       5     27492

十一.函数kstest()

1. 语法

$H = kstest(X)$
$H = kstest(X,cdf)$
$H = kstest(X,cdf,alpha)$
$H=kstest(X,cdf,alpha,tail)$
$[H,P,KSSTAT,CV] = kstest(X,cdf,alpha)$

2. 描述

H = kstest(X) %测试向量X是否服从标准正态分布，测试水平为5%。
H = kstest(X,cdf) %指定累积分布函数为cdf的测试(cdf=[ ]时表示标准正态分布)，测试水平为5%
H = kstest(X,cdf,alpha) % alpha为指定测试水平H=kstest(X,cdf,alpha,tail) % tail=0为双侧检验， tail=1单侧(<)检验， tail=-1单侧(>) 检验
[H,P,KSSTAT,CV] = kstest(X,cdf,alpha) %P为原假设成立的概率，KSSTAT为测试统计量的值，CV为是否接受假设的临界值。

3. 参数

3.1 输入参数

x— 样本数据
Alpha— 重要性级别（0.05（默认）| 标量值，范围为（0,1））
CDF— 假设连续分布矩阵的 cdf | 概率分布对象
Tail— 备选假设的类型

3.2 输出参数

h—假设检验结果
如果为h = 1，则表明在Alpha重要性级别拒绝了原假设，即不是正态分布。
如果为h = 0，则表明在Alpha重要性级别上无法拒绝原假设，即是正态分布。
p— p值
较小的值对原p假设的有效性表示怀疑。
ksstat—测试统计
假设检验的检验统计量，作为非负标量值返回。
cv—临界值
临界值，作为非负标量值返回。

4. 注意

kstest适用于小样本，当数据过大时，检验拒绝的临界值非常小，结果往往是拒绝原假设。
各种检验方法适用范围如下：

chi2gof适合大样本，一般要求50个以上
kstest适于小样本，
lillietest用于正态分布，与kstest类似，适用于小样本
jbtest,是通过峰度、偏度检测正态分布的，适用用大样本。

十二.函数crosstab()

1.句法

$tbl = crosstab(x1,x2)$
$tbl = crosstab(x1,…,xn)$
$[tbl,chi2,p] = crosstab()$
$[tbl,chi2,p,labels] = crosstab()$

2.描述

tbl = crosstab(x1,x2) %返回一个交叉列表，tbl具有相同长度的两个向量，的，x1和x2。
tbl = crosstab(x1,…,xn) %返回一个多维交叉列表，tbl，对于多个输入向量数据，x1，x2，…， xn。
[tbl,chi2,p] = crosstab() %对于在每个维度上独立的测试，还返回卡方统计量pchi2及其p值。您可以使用任何以前的语法。ptbl
[tbl,chi2,p,labels] = crosstab() %还返回一个单元格数组，labels其中每个输入参数x1… 都包含一列标签xn。

3.概念

频数（Frequency），又称“次数”。指变量值中代表某种特征的数（标志值）出现的次数;

4.参数

输入参数

x1— 分组变量的输入向量
x2— 分组变量的输入向量
x1,…,xn— 输入向量

输出参数

tbl— 整数值的交叉列表表（矩阵）
chi2—卡方统计（正标量值）
p— p -Value（标量值，范围内[0,1]）
labels—数据标签（单元格数组）

5.例

1.tbl = crosstab(x1,x2)

x = [1 1 2 3 1];
y = [1 2 5 3 1];
tbl = crosstab(x,y)
%行表示x中出现的三个数值
%列表示y中出现的四个数值
%得到的表表示对应值出现的次数，例（1，1）
tbl =
     2     1     0     0
     0     0     0     1
     0     0     1     0

2.[tbl,chi2,p] = crosstab(x,y)

[table,chi2,p] = crosstab(x,y)
    table =
         2     1     0     0
         0     0     0     1
         0     0     1     0
    chi2 =
        10
    p =
        0.1247

十三.zscore函数数据的标准化处理

1.简介

在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。数据标准化的方法有很多种，常用的有“最小—最大标准化”、“Z-score标准化”和“按小数定标标准化”等。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。

2.z-score 标准化

这种方法基于原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。
z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。

3.计算公式

新数据=（原数据-均值）/标准差
用zscore函数可以把数据进行z-score标准化处理。

4.用法

$Y=zscore(X)$

x为标准化之前的数据，y为标准化后的数据

5.特点：

样本平均值为0，方差为1；
区间不确定，处理后各指标的最大值、最小值不相同；
对于指标值恒定的情况不适用；
对于要求标准化后数据大于0 的评价方法（如几何加权平均法）不适用。

参考文章

学习 > 数学建模

#数学建模 #matlab

matlab学习

https://blog.baixf.tk/2020/09/01/数学建模/matlab学习/

作者

白小飞

发布于

2020年9月1日

许可协议

Class 1 达摩院视觉AI技术应用探索上一篇

学习常用模型及算法4.元胞自动机下一篇