学习常用模型及算法3.遗传算法

1.简介

遗传算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传, 突变, 自然选择(适者生存，优胜劣汰遗传机制) 以及杂交等。当然借鉴这些现象主要是因为这些现象的某些特性，而不仅仅是现象本身。所以理解这些现象的特性对于理解算法的思想是至关重要的。
在遗传算法中，问题域中的可能解被看作是种群的个体。对于一个最优化问题，一定数量的候选解（称为个体）的抽象表示（称为染色体）的种群向更好的解进化。传统上，解用二进制将个体编码成符号串形式（即0 和1 的串），但也可以用其他表示方法。进化从完全随机个体的种群开始，之后一代一代发生。在每一代中, 整个种群的适应度被评价，基于它们的适应度，从当前种群中随机地择优选择多个个体。通过杂交和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。从而不断得到更优的种群，同时搜索优化种群中的最优个体，求得满足要求的最优解。
选择可以使得种群在一定程度上淘汰一些较差的解，这样就减少了以后计算的消耗。交叉和变异，在一定程度上保留了本代种群的优良特性（也就是解的优化性），并且基于本代优良特性产生的下一代种群不至于会有很差的优化性，这样就减少了搜索的代价。
遗传算法可以认为是退火算法的更加复杂化，能够使用遗传算法的地方就能够使用退火算法。如果遗传算法的种群只有一个个体，并且去除算法中的选择和交叉，仅保留变异操作，那么这两个算法是非常类似的。正是因为遗传算法使用了种群这个机制，使得它可以并行操作，在同一时间内可以求解一定数量的最优个体。而退火算法在同一时间内只能优化一个方案。这也就是它们两者的区别。根据实际问题的需要，一般都是先选退火算法。

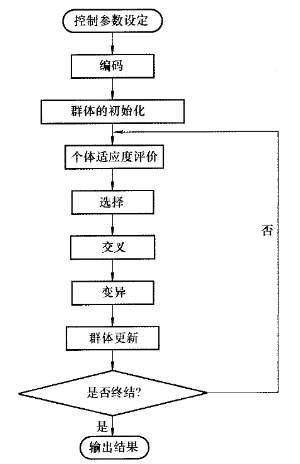
2.算法模型

算法的主要步骤

  1. 初始化: 初始化进化代数计数器（generation） t ←← 0（即初始值为0），最大进化代数（max_generation）TT。随机生成MM个个体作为初始群体P(t)P(t)（population）。其中MM就是种群大小（population_size），TT就是进化代数（max_generation）。
  2. 个体评价：计算P(t)P(t) 中各个个体的适应度值（population_fitness）。适应度值是一个M×1M×1维的向量。每个维度对应每个个体的适应度值。
  3. 选择运算：将选择算子（select）作用于群体。
  4. 交叉运算：将交叉算子（crossover）作用于群体。
  5. 变异运算：将变异算子（mutate）作用于群体，并通过以上运算得到下一代群体P(t+1)P(t+1)。
  6. 终止条件：如果t≤Tt≤T，则t←t+1t←t+1并跳转到第2步；否则输出P(t)P(t)中的最优解。也就是没有迭代完最大的迭代次数，那么继续迭代，并且代际更新。否则，就结束

3.主要内容

  • 解空间和编码
    编码是解的表达形式，解空间的表达依赖于编码形式。编码影响交叉和变异等运算，在一定程度上会影响算法的效率。编码的形式主要有：二进制编码，实数编码，符号编码，格雷编码。选得较多的有实数编码，计算简答， 而且便于理解。

  • 适应度计算
    适应度是算法进行淘汰的依据，也就是说，适应度一般都是非负的，通常由目标函数直接改造得到，比如目标函数的相反数，目标函数的倒数。适应度函数不应该太复杂，以免影响计算。

  • 选择算子
    主要的方法有轮盘赌（比例选择算子），两两竞争，排序竞争。使用较多的就是前两个了。选择主要的作用就是从父代中选择一些适应度高的个体遗传到后代中。而且这是一个随机选择，依概率选择，适应度高的被选择的可能性大，适应度低的个体被选择的可能性小。

  • 交叉算子
    交叉就是指两个相互配对的染色体（在实际中一般选择相邻的两个染色体）依据交叉概率，交换他们的部分基因，从而形成新个体。通俗来讲，就是一个个体与其相邻的个体依据某个概率交换部分元素，从而产生新个体的过程。这样的过程会保留交换之前的个体的优良特性，减少算法的计算开销。遗传算法的独特之处，不仅仅是遗传算法，模拟退火算法等的独特之处都是其产生新个体的方式。而交叉运算是遗传算法产生新个体的主要方法，所以交叉运算是遗传算法的关键之处。交叉主要有两种，单点交叉和两点交叉，两点交叉使用的较多。

  • 变异算子
    变异操作对种群中的个体的某些基因上的基因值作变动，模拟生物在繁殖过程中新产生的染色体中的基因会以一定的概率出错。通俗来讲，就是一个个体的随机选取的某些元素依据某种概率发生变化。变异运算是产生新个体的辅助方法，决定遗传算法的局部搜索能力， 保持种群多样性。交叉运算和变异运算的相互配合，共同完成对搜索空间的全局搜索和局部搜索。类型主要有基本位变异和换位变异。

  • 程序实现
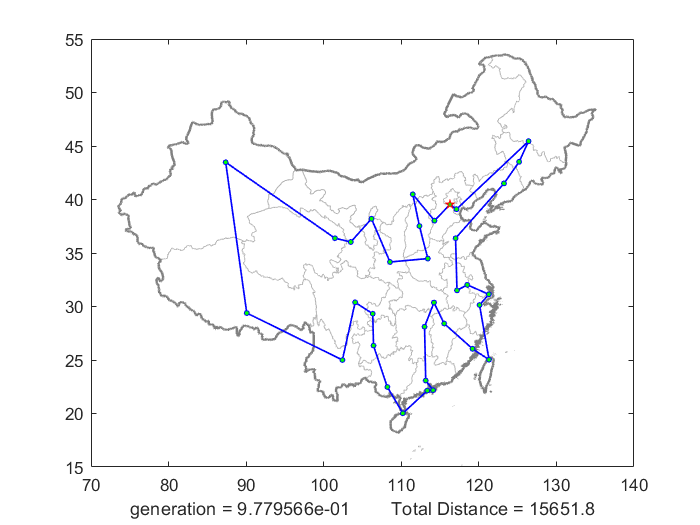
    这是解决TSP问题的程序，主要用于演示
    程序框架介绍：

  1. 清理工作空间，加载数据，画出底层画布
  2. 计算各城市之间的距离矩阵（distance_matrix），若城市有CC个则矩阵应该是C×CC×C的。
  3. 初始化变量。包括种群大小（population_size），最大代数（max_generation），变异概率（probability_mutate）。
  4. 初始化一个矩阵，用于存储种群。这就是种群的数学表示。（population或population_matrix）
  5. 迭代开始。
  6. 评价准则。计算每个个体的适应度。在这个问题中，个体的适应度等于个体的目标函数的倒数。其中涉及到目标函数值向量（f_vector），适应度向量（population_fitness）。
  7. 获取本代种群中适应度最高的那个个体，并且加到下一代中。
  8. 选择操作。这里使用的是两两竞争。将种群中的个体随机打乱，生成两个随机序列，并依次比较这两个随机序列，选择相应位置上适应度较高的个体，可能会出现重复，即使出现重复但都是适应度较高的方案，经过交叉和变异，会生成不同的个体，对结果影响不大。
  9. 交叉操作。取种群中的个体，两两相取。这里使用的是两点交叉，所以随机生成两个点，在这两个点之间进行交叉操作。而交叉的对象就是这两个同时取到的个体，交叉之前的是父代，交叉之后的是子代。
  10. 变异操作。每个个体是依概率进行变异的，这就说明有的个体可能不会变异。 而变异的方式也是随机的，这就能较好的符合真实的自然现象。三种变异方式：随机的两个点进行交换（也就是单个个体随机选取两个元素进行交换），两个点之间的数据循环移动（包括左移位，右移位），两个带你之间的数据转置（这是使用概率较大的一种变异方式，约为0.5）。

4.例

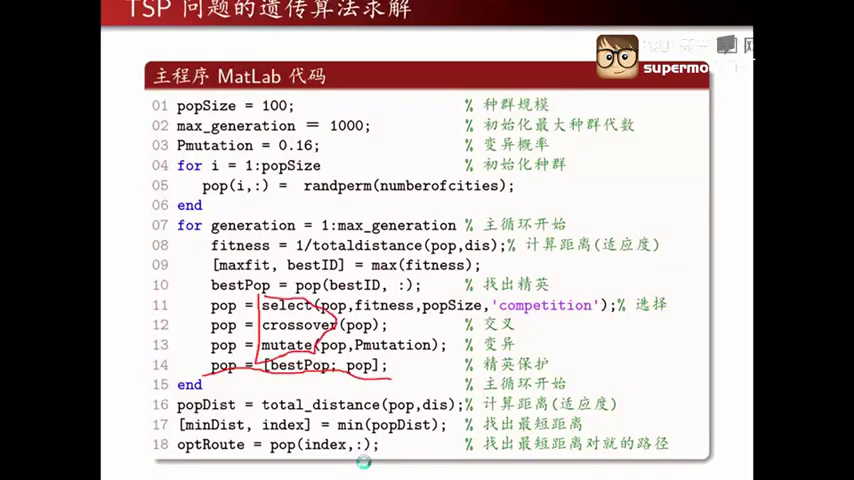
pop为初始化的种群
select选择 crossover交叉 mutate变异
第14行是为了将最好的解留在种群当中

size(pop, 1)求出pop的行数，即种群的个数
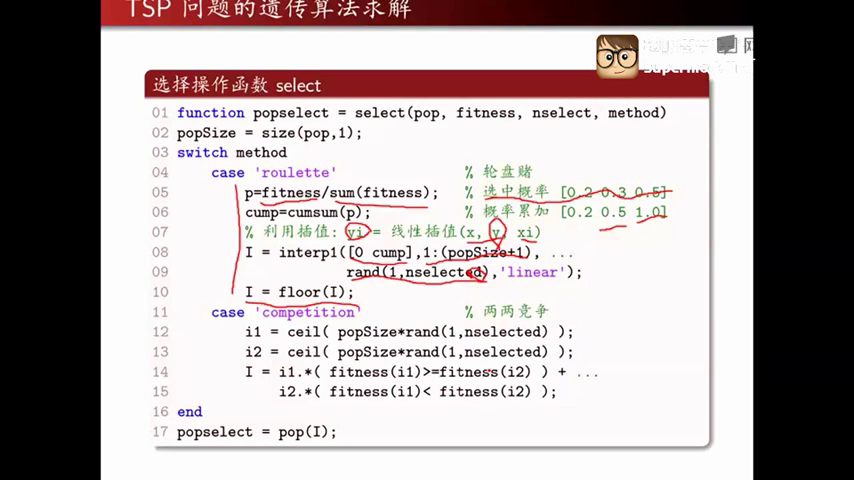
第12行可理解为：在1至popSize的整数之间任意挑选nselect次（可重复）之后组成的数组。
interp1为线性插值函数
I是我们选择的行数，即我们选择了哪些个体。

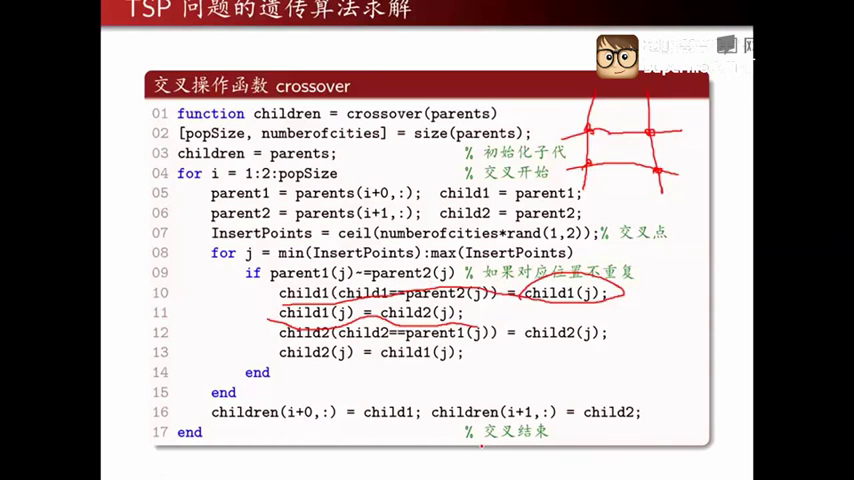
InsertPoints决定了我们进行交叉操作的起点与终点。
具体交叉方式与前文所述类似。
待交叉结束后，将child1和child2插回children。

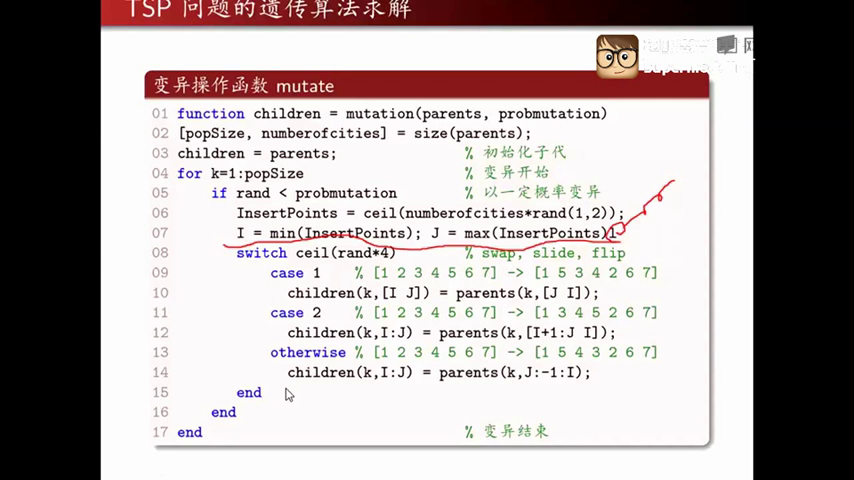
当rand小于probmutation时，发生变异，变异情况有三种，1/4的可能性swap，1/4的可能性slide，1/2的可能性flip。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
%
% This is the main script to finds a (near) optimal solution to the Traveling
% Salesman Problem (TSP), by setting up a Simulated Annealing (SA) to search
% for the shortest route (least distance for the salesman to travel to each
% city exactly once and return to the starting city).
%
% Author: zhou lvwen       Email: zhou.lv.wen@gmail.com
% Release Date: November 12, 2012
%
clear;clc;
load china; % geographic information
plotcities(province, border, city); % draw the map of China
numberofcities = length(city);      % number of cities
% distance matrix: dis(i,j) is the distance between city i and j.
dis = distancematrix(city);
temperature = 1000;                 % Initialize the temperature.
cooling_rate = 0.94;                % cooling rate
iterations = 1;                     % Initialize the iteration number.
% Initialize random number generator with "seed".
rand('seed',0);
% Initialize the route by generate a sequence of random
route = randperm(numberofcities);
% This is objective function, the total distance for the routes.
previous_distance = totaldistance(route,dis);
% This is a flag used to cool the current temperature after 100 iterations
temperature_iterations = 1;
% This is a flag used to plot the current route after 200 iterations
plot_iterations = 1;
% plot the current route
plotroute(city, route, previous_distance, temperature);
while 1.0 < temperature
    % generate randomly a neighbouring solution
    temp_route = perturb(route,'reverse');
    % compute total distance of the temp_route
    current_distance = totaldistance(temp_route, dis);
    % compute change of distance
    diff = current_distance - previous_distance;
    % Metropolis Algorithm
    if (diff < 0) || (rand < exp(-diff/(temperature)))
        route = temp_route;         %accept new route
        previous_distance = current_distance;
        % update iterations
        temperature_iterations = temperature_iterations + 1;
        plot_iterations = plot_iterations + 1;
        iterations = iterations + 1;
    end
    % reduce the temperature every 100 iterations
    if temperature_iterations >= 100
       temperature = cooling_rate*temperature;
       temperature_iterations = 0;
    end
    %  plot the current route every 200 iterations
    if plot_iterations >= 200
       plotroute(city, route, previous_distance,temperature);
       plot_iterations = 0;
    end
end
% plot the final solution
plotroute(city, route, previous_distance,temperature);

5.算法的比较

基于TSP问题，我们最先想到的就是暴力搜索方法，就是遍历所有可能的情况，然后计算每种情况的代价，选择其中代价最小的一种情况作为最优解，这在理论上是一定能够找到最优解的，然后解空间非常大，遍历所有情况花费的时间可能是无穷的，这种情况下，实际上是不可能实现的。遗传算法区别于这种暴力搜索的一个关键就是，它在随机搜索解空间中新的解的时候，能够保留原解的优良特性，不至于本次搜索到了一个比较好的解，接下来会搜索很多比本次的解还要差的解，而暴力搜索就会产生这样的过程，即在搜索到一个较好的解之后，还可能会搜索很多比这个解要差很多的解。
那么在算法上这样搜索解的过程就是产生新个体的过程，或者可以叫做是邻解生成，在模拟退火中，主要通过扰动产生新解，这个过程类似于遗传算法的变异，而变异过程只是遗传算法产生新个体（新解）的辅助方法，主要方法是交叉。而选择又使得一些适应度较低的个体，也就是代价较大的解被抛弃掉，在算法中叫做淘汰。而不论是扰动，变异，还是交叉，选择，都达到了两个目的，一个是减少需要被搜索的解空间，另一个是保留较优的解。选择在减少需要被搜索的解空间上达到的效果最明显，而其他三种在保留较优的解上达到的效果比较明显。
所以，基于这些算法，我们改进暴力搜索的方向应该是加上限制，使得这些限制能够减少被搜索的解空间，并且能够在被搜索的解空间中尽可能多的保留较优的解。另外，受这些算法的启发，我们在优化一个比较暴力的方案时（或者说是一个比较粗糙的类全解空间搜索方案），也可以在这样的方向上加上一些措施，以减少我们做的无用功，也就是使得我们尽可能的朝着最优解的方向前进，而不是在中途后退，去检验较差的解是否可行。

参考文章

  1. 遗传算法—-学习反馈 ↩
  2. 学习常用模型及算法：1.启发式算法（模拟退火和遗传算法） ↩
学习 > 数学建模
#数学建模 #matlab
学习常用模型及算法3.遗传算法
https://blog.baixf.tk/2020/08/23/数学建模/学习常用模型及算法3.遗传算法/
作者
白小飞
发布于
2020年8月23日
许可协议