单因素方差分析
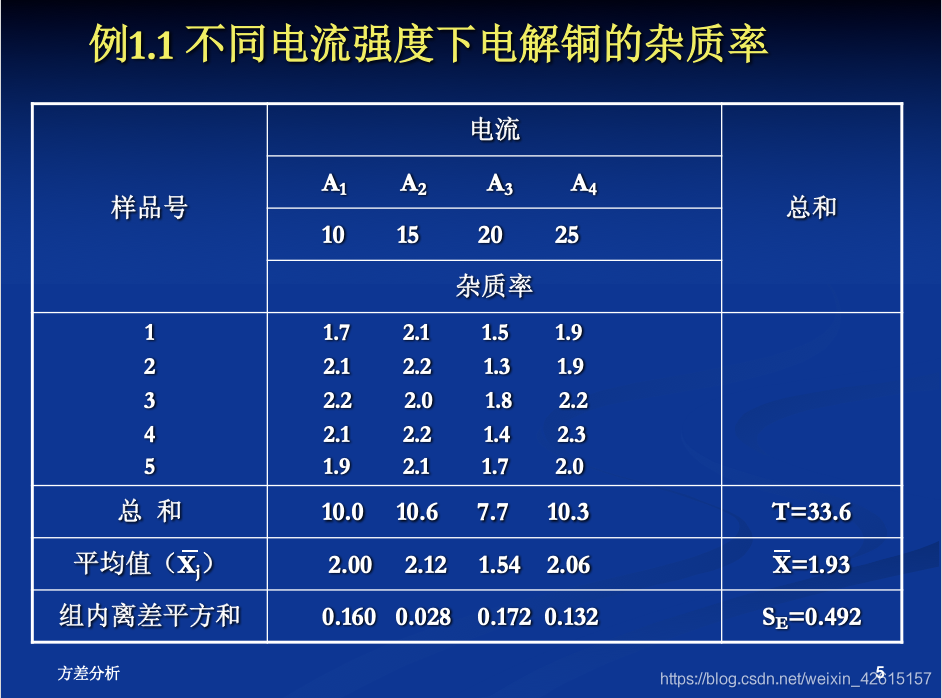
例
正态性检验
原假设为不同样品的电流是符合正态分布的。
备择假设为不同样品的电流是符合正态分布的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| a=[1.7 2.1 1.5 1.9
2.1 2.2 1.3 1.9
2.2 2.0 1.8 2.2
2.1 2.2 1.4 2.3
1.9 2.1 1.7 2.0];
b=[1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5];
a=reshape(a',numel(a),1);
for i=1:5
ai=a(b==i);
alpha=0.05;
[mui,sigmai]=normfit(ai);
pi=normcdf(ai,mui,sigmai);
[h0(i),p(i)]=kstest(ai,[ai,pi],alpha);
end
h0,p
|
1
2
3
4
5
| h0 =
1×5 logical 数组
0 0 0 0 0
p =
0.9807 0.8446 0.8207 0.6162 0.9499
|
h0均为0,接受原假设,即每个样本的电流均符合正态分布。
方差齐性检验
原假设是5个样本电流数据服从方差相同的正态分布。
备择假设是服从方差不同的正态分布。


p>>0.05,所以接受原假设,所以5个样本服从方差相同的正态分布。
方差分析
原假设是没有显著差异,即$μ_1=μ_2=μ_3=μ_4=μ_5$。
备择假设时有显著差异。
1
| [p,table,stats]=anova1(a,b)
|


p>>0.05,接受原假设,即没有显著差异。
两两之间多重比较
1
| sta=multcompare(stats,'estimate','column')
|
1
2
3
4
5
6
7
8
9
10
11
| sta =
1.0000 2.0000 -0.7385 -0.0750 0.5885 0.9965
1.0000 3.0000 -0.9135 -0.2500 0.4135 0.7711
1.0000 4.0000 -0.8635 -0.2000 0.4635 0.8805
1.0000 5.0000 -0.7885 -0.1250 0.5385 0.9758
2.0000 3.0000 -0.8385 -0.1750 0.4885 0.9221
2.0000 4.0000 -0.7885 -0.1250 0.5385 0.9758
2.0000 5.0000 -0.7135 -0.0500 0.6135 0.9993
3.0000 4.0000 -0.6135 0.0500 0.7135 0.9993
3.0000 5.0000 -0.5385 0.1250 0.7885 0.9758
4.0000 5.0000 -0.5885 0.0750 0.7385 0.9965
|

经两两之间多重验证,各样本没有显著差异,即$μ_1=μ_2=μ_3=μ_4=μ_5$
参考





