每日一题【20200803】

两变量间的相关系数

例

某地区1982~1996年国民生产总值与工商税收收入的数据如下: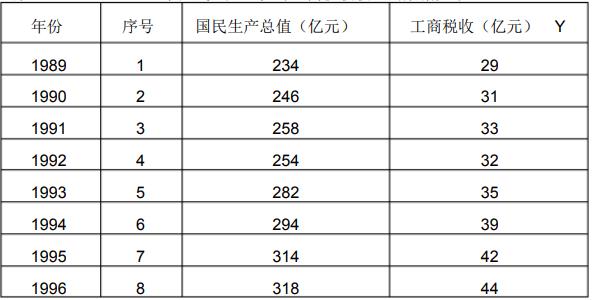

计算两变量的相关系数

K-S test正态检验

x=[234 246 258 254 282 294 314 318]
y=[29 31 33 32 35 39 42 44]
x=x'
y=y'
[mu1,sigma1]=normfit(x)
[mu2,sigma2]=normfit(y)
p1=normcdf(x,mu1,sigma1)
p2=normcdf(y,mu2,sigma2)
h1=kstest(x,[x,p1])
h2=kstest(y,[y,p2])

h1 =
  logical
   0
h2 =
  logical
   0

返回值均为0，说明接受假设，两个序列均为正态序列。
但是分析该数据不是连续型数据，所以不能用Pearson检验，所以采用Spearman检验和Kendall检验。

统计学中，连续数据，离散数据又称连续变量，离散变量。区分两种变量的方法为观察变量是否连续可分。连续变量，指在一定区间内可以任意取值，相邻的两个数值可作无限分割(即可取无限个值)。比如题主所说的身高，身高可以是183，也可以是183.1，也可以是183.111……1。离散变量，是指其数值只能用自然数、整数、计数单位等描述的数据。例如，职工个数(总不能是1.2个吧)，成绩A+等。
要区分每月核心行为 1 次、 2次、3次，对于大多数产品意义不是很大。倒不如将连续数据转换为离散，比如 5 次以下归为一类，5 次以上归为另一类。更好的做法用「二八」划分，比如以累计贡献度达 80 % 的用户核心操作数值作为界线划分「高低」用户。即使 1、2、3次意义重大，那转为离散会更合适，每个数值能区分出不同意义。

通过阅读相关文献，我发现可能是我理解错了qwq,也许这是连续性的数据！！！

• 读取数据
• 调用函数进行检验
• 该数据不存在第三因素，所以我们不进行偏相关系数（qwq打脸）

x=[234 246 258 254 282 294 314 318]
y=[29 31 33 32 35 39 42 44]
z=[1 2 3 4 5 6 7 8]
x=x'
y=y'
z=z'
[r,p]=corr(x,y,'type','pearson') %R检验（<0.05）
[r,p]=partialcorr(x,y,z)
[r,p]=corr(x,y,'type','spearman') %T检验
[e,p]=corr(x,y,'type','kendall') %正态检验

r =
    0.9884
p =
   3.8806e-06
r =
    0.7921
p =
    0.0337
r =
     1
p =
   4.9603e-05
e =
     1
p =
   4.9603e-05

参考

1. 如何判断特征是连续的还是离散的? ↩
2. 数据|连续还是离散 ↩