随机序列的Markov链预测
例
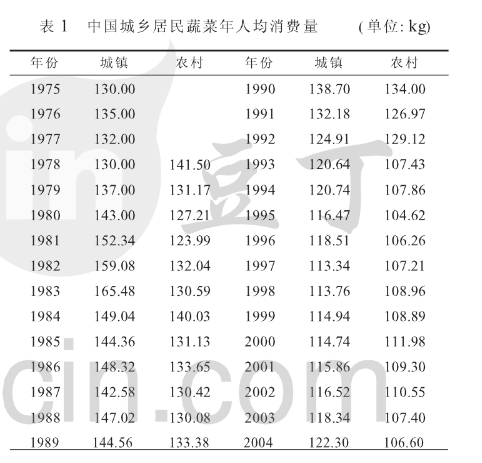
1978年至2004年城镇居民蔬菜人均消费数据,请给出城镇居民蔬菜消费量的长期趋势。
1.状态划分及构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| A=[130 137 143 152.34 159.08 165.48 149.04 144.36 148.32 142.58 147.02 144.56 138.70 132.18 124.91 120.64 120.74 116.47 118.51 113.34 113.76 114.94 114.74 115.86 116.52 118.34 122.30];
b=diff(A);
A1=A(1:end-1);
tt=b./A1*100;
z=[-3 0 3];
for i=1:length(tt)
if tt(i)<z(1)
aa(i)=1;
elseif tt(i)<z(2)
aa(i)=2;
elseif tt(i)<z(3)
aa(i)=3;
else
aa(i)=4;
end
end
|
2.计算各状态转移次数及转移概率
1
2
3
4
5
6
7
8
9
10
11
12
13
| for i=1:4
for j=1:4
k=[i,j];
c(i,j)=length(strfind(aa,k));
end
end
c
cs=sum(c,2);
p=zeros(4,4);
for i=1:4
p(i,:)=c(i,:)./cs(i);
end
p
|
1
2
3
4
5
6
7
8
9
10
| c =
4 0 4 1
1 0 1 0
3 1 3 1
1 1 0 4
p =
0.4444 0 0.4444 0.1111
0.5000 0 0.5000 0
0.3750 0.1250 0.3750 0.1250
0.1667 0.1667 0 0.6667
|
3.计算城镇居民年人均蔬菜消费量的长期趋势
(极限分布)

1
2
3
4
| p1=p'-eye(size(p'));
p2=[p1;ones(1,4)];
b11=[zeros(1,4),1]';
x=linsolve(p2,b11)
|
1
2
3
4
5
| x =
0.36
0.08
0.32
0.24
|
参考





