每日一题【20200730】

灰色预测案例分析

例

由1990-2001年某地蔬菜产量，建立模型预测该地2002年蔬菜产量，并对预测结果做检。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
(1)编写函数文件
function [x,c,error1,error2]=GM11(x0,k)
%其中x0为输入序列,k为预测长度
%x为预测输出序列，c为后检验检验数
%error1为残差，error2为相对误差
%format long； %精度达到软件最大值
n=length(x0);
x1=[];
x1(1)=x0(1);
for i=2:n
    x1(i)=x1(i-1)+x0(i); %计算累加生成序列
end
for i=1:n-1 %求紧邻矩阵
    B(i,1)=-0.5*(x1(i)+x1(i+1));
    B(i,2)=1;
    Y(i)=x0(i+1);
end
alpha=(B'*B)^(-1)*B'*Y'; %做最小二乘估计求出参数
a=alpha(1,1);
b=alpha(2,1);
d=b/a;
c=x1(1)-d;
x2(1)=x0(1);
for i=1:n-1
    x2(i+1)=c*exp(-a*i)+d;
    x(i+1)=x2(i+1)-x2(i);
end %计算时间响应参数函数
for i=(n+1):(n+k)
    x2(i)=c*exp(-a*(i-1))+d;
    x(i)=x2(i)-x2(i-1);
end %计算预测序列
for i=1:n
    error(i)=x(i)-x0(i);
    error1(i)=abs(error(i)); %计算残差 <20%
    error2(i)=error1(i)/x0(i); %计算相对误差
end
c=std(error1)/std(x0); %计算后验差检验数
1
2
3
4
(2)matlab操作代码
y=[19519,19578,19637,19695,16602,25723,30379,34473,38485,40514,42400,48337];
k=1;
[X1,c1,e1,e2]=GM11(y,k)
1
2
3
4
5
6
7
结果展示
-------------------------------------累加后序列--------------------------------
x1 =
  列 1 至 9
       19519       39097       58734       78429       95031      120754      151133      185606      224091
  列 10 至 12
      264605      307005      355342
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
------------------------------------x1的紧邻矩阵----------------------------------
B =
   1.0e+05 *
   -0.2931    0.0000
   -0.4892    0.0000
   -0.6858    0.0000
   -0.8673    0.0000
   -1.0789    0.0000
   -1.3594    0.0000
   -1.6837    0.0000
   -2.0485    0.0000
   -2.4435    0.0000
   -2.8580    0.0000
   -3.3117    0.0000
Y =
  列 1 至 9
       19578       19637       19695       16602       25723       30379       34473       38485       40514
  列 10 至 11
       42400       48337
1
2
3
4
5
6
7
8
9
10
11
12
13
----------------------------------最小二乘法的参数--------------------------
a =
   -0.1062
b =
   1.4000e+04
</code></pre>
<pre><code class="language-matlab line-numbers">-------------------------------------预测序列----------------------------------
x =
   1.0e+04 *
  列 1 至 11
         0    1.6958    1.8858    2.0971    2.3321    2.5934    2.8840    3.2072    3.5666    3.9662    4.4107
  列 12 至 13
    4.9049    5.4546
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
--------------------------------------残差值-------------------------------------
error1 =
   1.0e+04 *
  列 1 至 11
    1.9519    0.2620    0.0779    0.1276    0.6719    0.0211    0.1539    0.2401    0.2819    0.0852    0.1707
  列 12
    0.0712
-----------------------------------残差值相对误差--------------------------------
error2 =
  列 1 至 11
    1.0000    0.1338    0.0397    0.0648    0.4047    0.0082    0.0506    0.0696    0.0733    0.0210    0.0403
  列 12
    0.0147
-----------------------------------后验差检验数--------------------------------
c =
    0.4879

列数据

1
2
3
4
5
6
fprintf('%s\n','-----------------1991-2001年GM(1,1)灰色系统预测值与实际值比较---------------')
fprintf('   %s              %s            %s            %s           %s\n','年份','预测值','实际值','残差','相对误差');
for i=2:12
fmt='  %d  %20.4f  %15.4f  %15.4f  %13.4f\n';
fprintf(fmt,t(i),X1(i),y(i),e1(i),e2(i));
end
1
2
3
4
5
6
7
8
9
10
11
12
13
----------------1991-2001年GM(1,1)灰色系统预测值与实际值比较---------------
   年份              预测值            实际值            残差           相对误差
  1991            16957.6939       19578.0000        2620.3061         0.1338
  1992            18857.9037       19637.0000         779.0963         0.0397
  1993            20971.0433       19695.0000        1276.0433         0.0648
  1994            23320.9727       16602.0000        6718.9727         0.4047
  1995            25934.2255       25723.0000         211.2255         0.0082
  1996            28840.3088       30379.0000        1538.6912         0.0506
  1997            32072.0359       34473.0000        2400.9641         0.0696
  1998            35665.8972       38485.0000        2819.1028         0.0733
  1999            39662.4718       40514.0000         851.5282         0.0210
  2000            44106.8863       42400.0000        1706.8863         0.0403
  2001            49049.3236       48337.0000         712.3236         0.0147

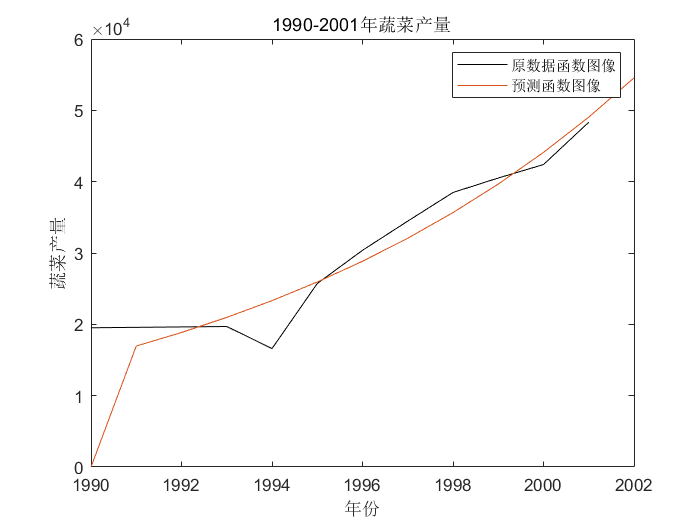
绘制图像

1
2
3
4
5
6
7
8
t=[1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002]
plot(t(1:12),y,'k','Markersize',10)
hold on
plot(t,X1)
legend('原数据函数图像','预测函数图像')
xlabel('年份')
ylabel('蔬菜产量')
title('1990-2001年蔬菜产量')

参考

  1. NULL ↩
学习 > 数学建模
#数学建模 #灰色系统预测 #GM11 #后检验 #后验差检验数 #相对误差 #残差 #最小二乘法 #预测序列
每日一题【20200730】
https://blog.baixf.tk/2020/07/30/每日一题/每日一题【20200730】/
作者
白小飞
发布于
2020年7月30日
许可协议