每日一题【20200725】

时间序列的ARIMA预测分析

例

假设我们有这么一段数据（采样自移动公司某段时间的开户客户数目），预测接下来31天的开户客户数。

文件地址： 链接: https://pan.baidu.com/s/1RS-x1HTQLUU1IF5g3Yesdw 提取码: xbyt

在这里，我们把时间序列数据利用Cramer分解定理将其分解为以下四项： 
1
2
3
4
5
真实数据=趋势项+周期项+信息传递项+白噪声项
趋势性：例如随时间变化的一次函数/多次函数/幂函数趋势等
周期项：周期规律
信息传递项：
白噪声项：作为残差
## 1.观测数据（均值，周期等）
  • 读取数据
  • 绘制数据图像
  • 绘制自相关图像
1
2
3
4
5
6
7
8
9
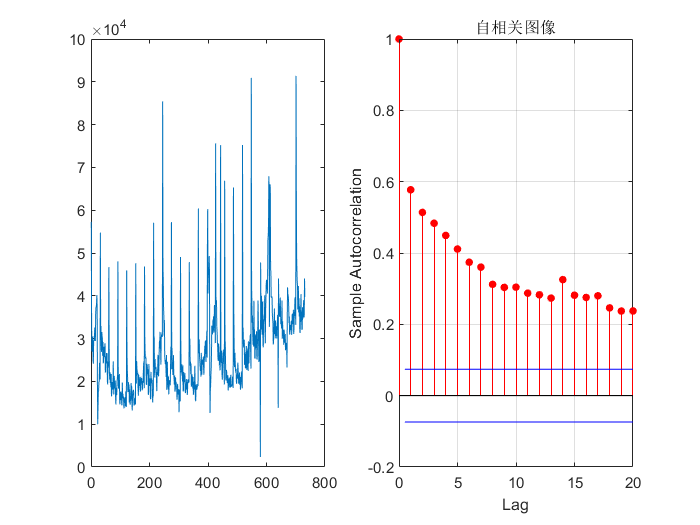
x0=xlsread('移动通知户开户数.xlsx','B2:B732');
n=1:length(x0);
subplot(1,2,1);
plot(n,x0);
title('原始数据图像');
hold on;
subplot(1,2,2);
autocorr(x0);
title('自相关图');

2. 数据预处理

  • 去周期/趋势
  • 绘制数据图像
  • 绘制自相关图像

如图所示我们可以看到周期大约是30或31，由此我们也可以推测该数据是一个来自每天的开户统计数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
s=31; %周期s=31
n=31; %预报数据个数
m1=length(x0)
for i=s+1:m1
    y(i-s)=x0(i)-x0(i-s);
end
x1=diff(y)
m2=length(x1)
subplot(1,2,1)
plot(1:m2,x1)
title('')
hold on
subplot(1,2,2)
autocorr(x1)

adf检验处理后的数据平稳

1
2
3
4
5
6
7
8
9
10
[h1,p1,adf,ljz]=adftest(x1)
h1 =
  logical
   1
p1 =
   1.0000e-03
adf =
  -47.5009
ljz =
   -1.9413

结果表示一阶31步后的数据是平稳的。

3. 白噪声检验

1
2
3
4
5
6
7
8
9
10
11
12
yanchi=[6,12,18];
[H,pValue,Qstat,CriticalValue]=lbqtest(x1,'lags',yanchi);
fprintf('%15s%15s%15s','延迟阶数','卡方统计量','p值');
fprintf('\n');
for i=1:length(yanchi)
    fprintf('%18f%19f%19f',yanchi(i),Qstat(i),pValue(i));
    fprintf('\n');
end
           延迟阶数          卡方统计量             p值
          6.000000         200.496085           0.000000
         12.000000         209.963846           0.000000
         18.000000         235.502676           0.000000

p<0.1说明数据不是白噪声,可以进行aeima模型。

4. 模型检验

  • aic
  • bic
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
x1=x1';
LOGL=zeros(6,6); %Initialize
PQ=zeros(6,6);
for p=0:5
    for q=0:5
        model=arima(p,0,q); %指定模型结构
        [fit,~,logL]=estimate(model,x1);
LOGL(p+1,q+1)=logL;
        PQ(p+1,q+1)=p+q; %计算拟合参数的个数
    end
end
LOGL=reshape(LOGL,36,1);
PQ=reshape(PQ,36,1);
[aic,bic]=aicbic(LOGL,PQ+1,m2);
fprintf('AIC为：\n');%显示计算结果
reshape(aic,6,6) %储存36个模型AIC的值
fprintf('BIC为: \n');
reshape(bic,6,6) %储存36个模型BIC的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
AIC为：
ans =
   1.0e+04 *
    1.5207    1.4932    1.4859    1.4859    1.4859    1.4861
    1.4980    1.4858    1.4859    1.4843    1.4843    1.4864
    1.4917    1.4858    1.4850    1.4840    1.4851    1.4844
    1.4892    1.4858    1.4862    1.4852    1.4839    1.4843
    1.4876    1.4846    1.4862    1.4844    1.4841    1.4841
    1.4873    1.4850    1.4846    1.4845    1.4836    1.4833
BIC为:
ans =
   1.0e+04 *
    1.5211    1.4942    1.4873    1.4877    1.4882    1.4889
    1.4989    1.4872    1.4878    1.4865    1.4870    1.4896
    1.4931    1.4877    1.4872    1.4867    1.4883    1.4880
    1.4910    1.4881    1.4889    1.4884    1.4876    1.4883
    1.4899    1.4873    1.4894    1.4880    1.4882    1.4887
    1.4901    1.4882    1.4883    1.4886    1.4882    1.4883

寻找使AIC\BIC值最小的p值和q值（p、q值越小越好）
如果数值相同可尽量选择阶数较小。
p=q=5

5. 模型估计

1
2
3
4
p=input('输入阶数p=');
q=input('输入阶数q=');
model=arima(p,0,q);  %指定模型的结构
m=estimate(model,x1);  %拟合参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ARIMA(5,0,5) Model (Gaussian Distribution):
                  Value       StandardError    TStatistic      PValue
                __________    _____________    __________    __________
    Constant      -0.13876         5.2153       -0.026606       0.97877
    AR{1}         -0.62756         0.2344         -2.6773     0.0074222
    AR{2}          0.63226        0.23509          2.6894     0.0071576
    AR{3}          0.45155        0.16781          2.6909     0.0071264
    AR{4}         -0.21596        0.23391        -0.92326       0.35587
    AR{5}          0.14475       0.055125          2.6259     0.0086427
    MA{1}         -0.16113         0.2338        -0.68919        0.4907
    MA{2}          -1.1618       0.073341         -15.841    1.6094e-56
    MA{3}         0.080585         0.3241         0.24864       0.80364
    MA{4}          0.64061        0.12254          5.2276    1.7168e-07
    MA{5}         -0.39824        0.17684          -2.252       0.02432
    Variance    1.0281e+08     1.3326e-06      7.7147e+13             0

6. 模型检验

1
2
3
4
z=iddata(x1);
ml1=armax(z,[p,q]);
e=resid(ml1,z);  %拟合做残差分析
[H,pValue,Qstat,CriticalValue]=lbqtest(e.OutputData,'lags',6)
1
2
3
4
5
6
7
8
9
H =
  logical
   0
pValue =
    0.9795
Qstat =
    1.1455
CriticalValue =
   12.5916

说明残差是白噪声序列。

7. 预测

1
2
3
4
5
6
[yf,ymse]=forecast(m,n,'Y0',x1);
yhat=y(end)+cumsum(yf);  %求y的预报值
for j=1:n
    x0(m1+j)=yhat(j)+x0(m1+j-s);  %求x的预测值
end
xhat=x0(m1+1:end)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
xhat =
   1.0e+04 *
    9.4432
    6.1221
    5.4381
    4.6014
    4.6824
    4.3914
    3.7724
    4.0716
    4.1337
    4.0116
    3.8555
    3.7977
    3.8511
    3.2243
    3.4339
    3.4500
    4.0557
    3.9356
    3.6604
    3.6947
    3.2538
    3.4977
    3.6063
    3.8183
    3.5776
    3.9540
    3.9762
    3.5320
    3.8284
    4.2821
    4.3404

这就是接下来31天的预测客户数。

参考

  1. NULL ↩
学习 > 数学建模
#数学建模 #数据预处理 #白噪声检验 #时间序列 #预测 #ARIMA #读取数据 #稳定性检验 #拟合 #AIC #BIC #卡方统计
每日一题【20200725】
https://blog.baixf.tk/2020/07/24/每日一题/每日一题【20200801】/
作者
白小飞
发布于
2020年7月24日
许可协议